先做网站还是做APP电子商务与网络营销题库

二叉树概念

再看二叉树基本操作前，再回顾下二叉树的概念，

二叉树是：

1. 空树

2. 非空：根节点，根节点的左子树、根节点的右子树组成的。

从概念中可以看出，二叉树定义是递归式的 

二叉树构成：根 左子树 右子树构成的。

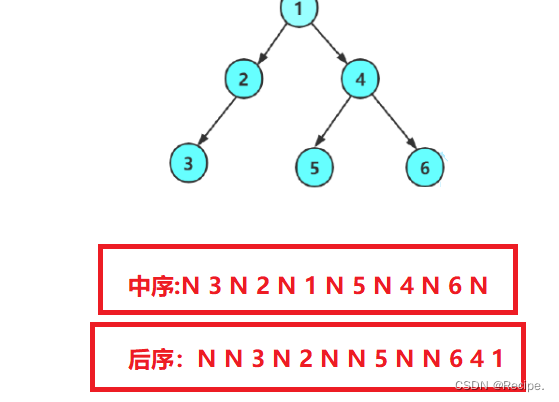
前序遍历是 ：根 左子树 右子树

中序遍历是 ：左子树 根 右子树

后序遍历是：左子树 右子树 根

根据上面的插图 前序遍历应该是: 1 2 3 N N N 4 5 N N 6 N N

那么你能试着说出中序和后序吗？

中序和后序如下图所示，你看你写对了吗？

我们学习普通链式二叉树的增删查改是没有意义的，因为我们现在学习普通链式二叉树是为了以后的搜索二叉树和AVL 红黑树打基础的，还有就是很多二叉树的题，都是出在普通链式二叉树结构。

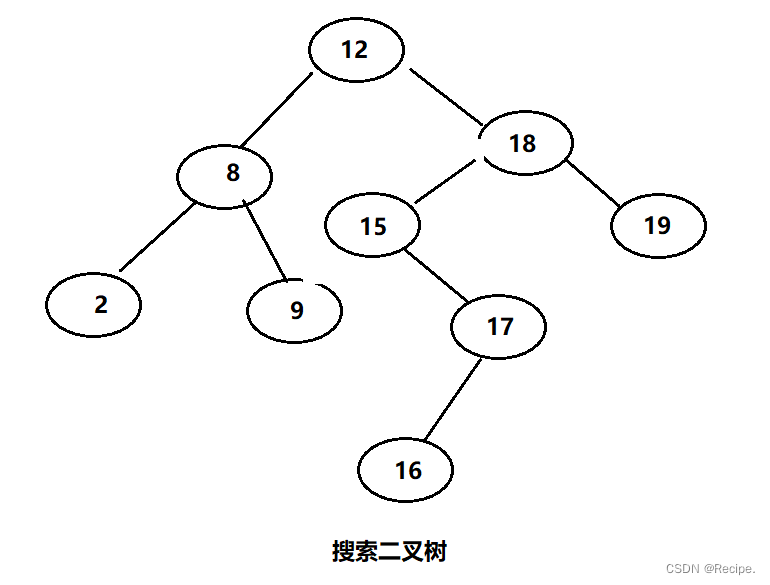
这是一个普通的搜索二叉树，二叉树的左子树比根小，右子树比根大。

如果搜索二叉树走中序遍历，就是个有序二叉树。

二叉树的构建

 在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入，为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。(注意：下述代码并不是创建二叉树的方式 )

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef struct BinaryTree
{struct BinaryTree* _left;struct BinaryTree* _right;int val;
}BTNode;BTNode* buynode(int x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->val = x;newnode->_left = NULL;newnode->_right = NULL;return newnode;
}
int main()
{BTNode* newnode1 = buynode(1);BTNode* newnode2 = buynode(2);BTNode* newnode3 = buynode(3);BTNode* newnode4 = buynode(4);BTNode* newnode5 = buynode(5);BTNode* newnode6 = buynode(6);newnode1->_left = newnode2;newnode2->_left = newnode3;newnode1->_right = newnode4;newnode4->_left = newnode5;newnode4->_right = newnode6;return 0;
}

二叉树的遍历 

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

前序遍历

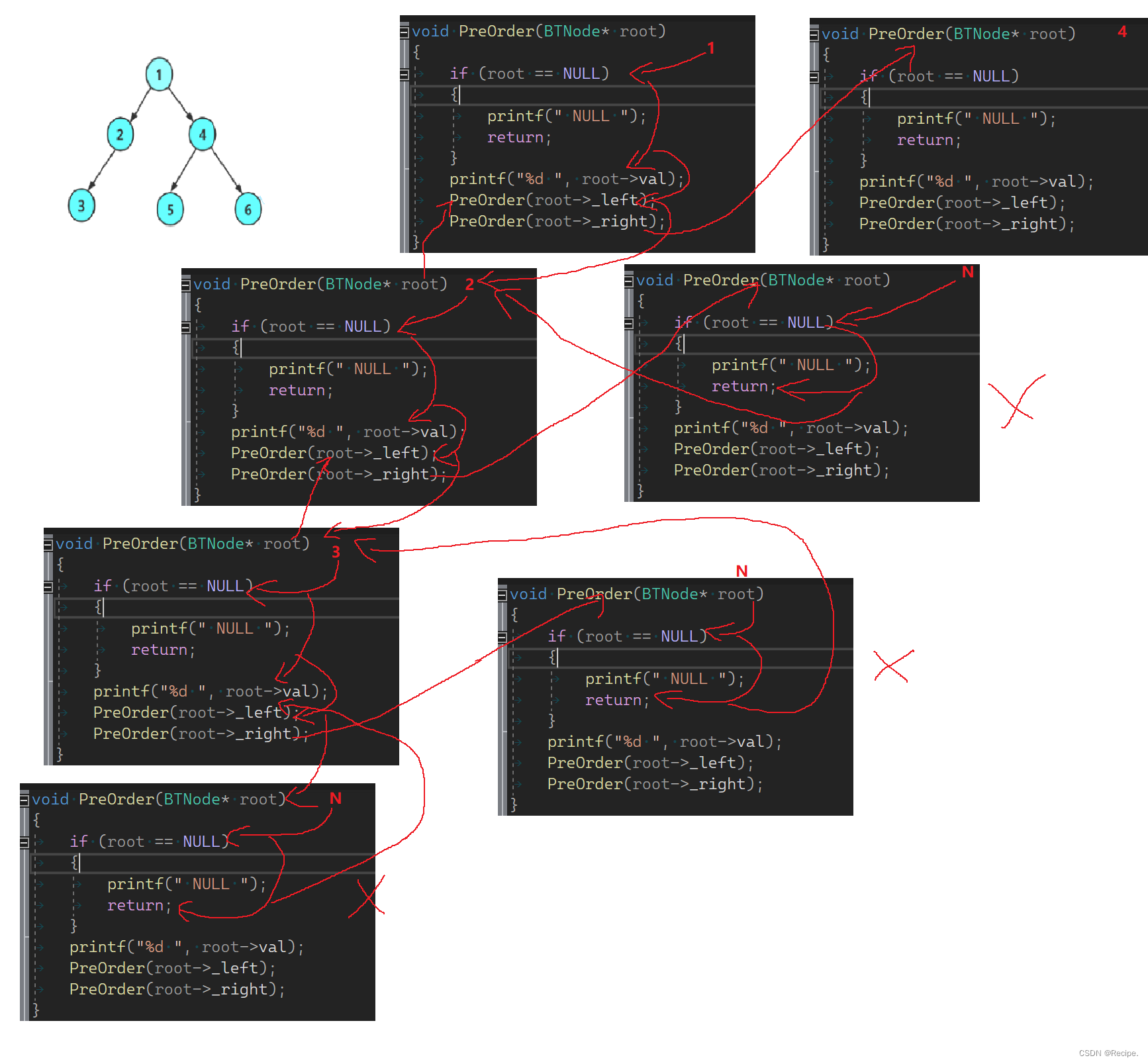
void PreOrder(BTNode* root)
{if (root == NULL){printf(" NULL ");return;}printf("%d ", root->val);PreOrder(root->_left);PreOrder(root->_right);
}

是不是觉得很简单？我们先运行下结果

跟我们之前预测的一模一样，为了更好的了解前序遍历，我画一下递归图。

 

中序遍历

就是把代码换个顺序就变成了中序遍历，为了深刻理解递归过程，建议像上面一样，自己画个递归过程理解。

void InOrder(BTNode* root)
{if (root == NULL){printf(" NULL ");return;}InOrder(root->_left);printf("%d ", root->val);InOrder(root->_right);
}

运行结果

 

后序遍历

void PostOrder(BTNode* root)
{if (root == NULL){printf(" NULL ");return;}PostOrder(root->_left);PostOrder(root->_right);printf("%d ", root->val);
}

 运行结果

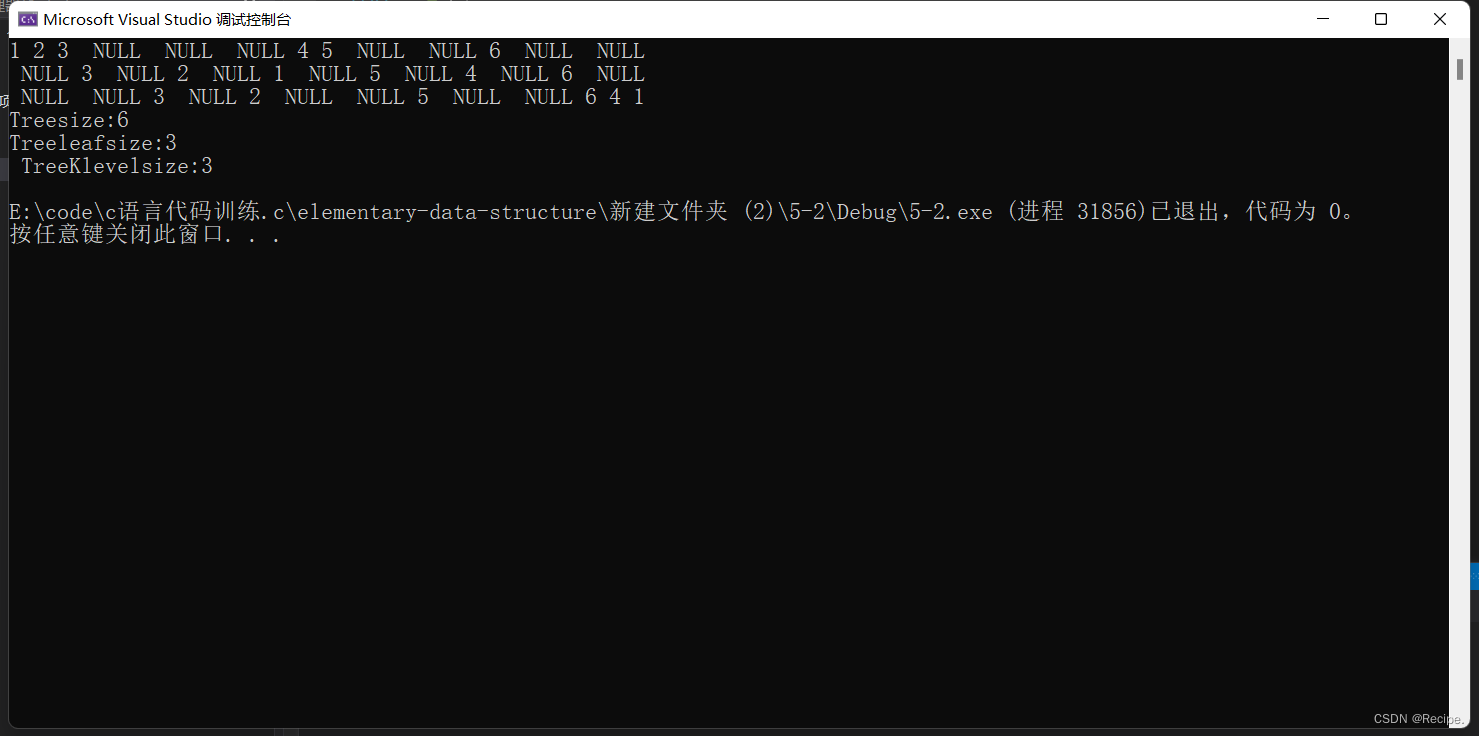
前序 中序 后序遍历结果

求节点个数以及高度等

二叉树的节点个数

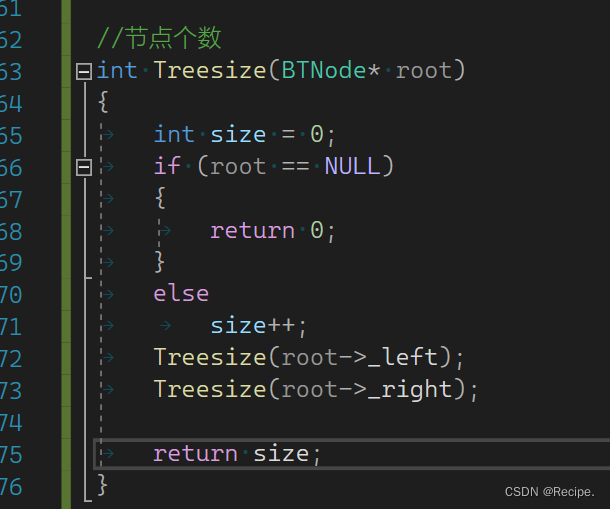
很多人可能都是想这么求节点个数的，但其实是错误的方法，因为size是局部变量 出了作用域就销毁了 根本求不出正确节点个数。

那么我们加上static 让它变成静态变量呢？

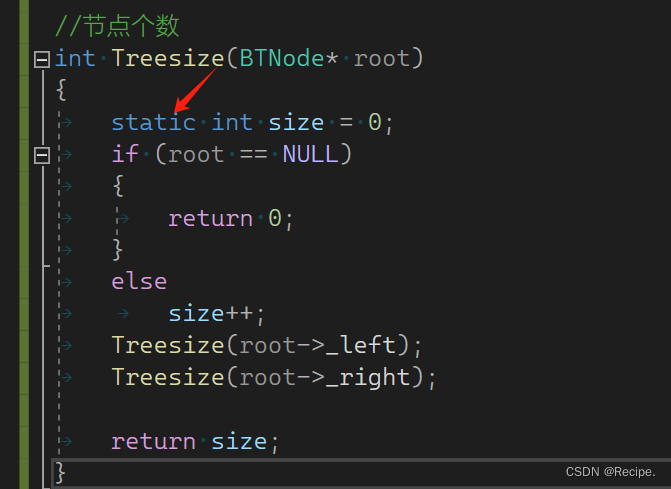
可以求出正确答案，因为静态变量在静态区，全局变量也在静态区，相当于一个全局变量，出了作用域并不会被销毁，而且只会走一次初始化，因此答案是正确的。

但有一个问题，如果我要再次调用这个函数求节点个数呢？

答案就会是错误的，因为静态变量只会走一次初始化。

解决办法也有，就是在前面把size设为全局变量 再次调用时归为0即可 答案还是6，但这种方法太low了。 

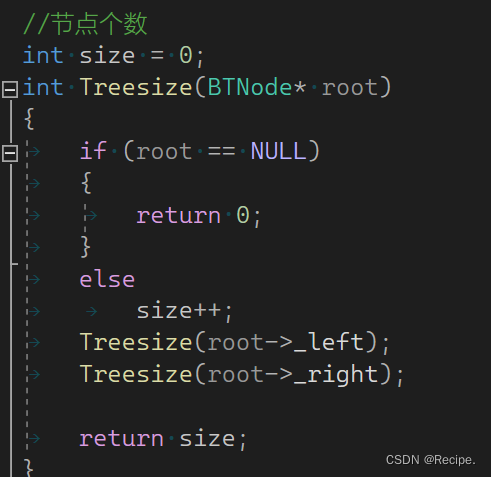
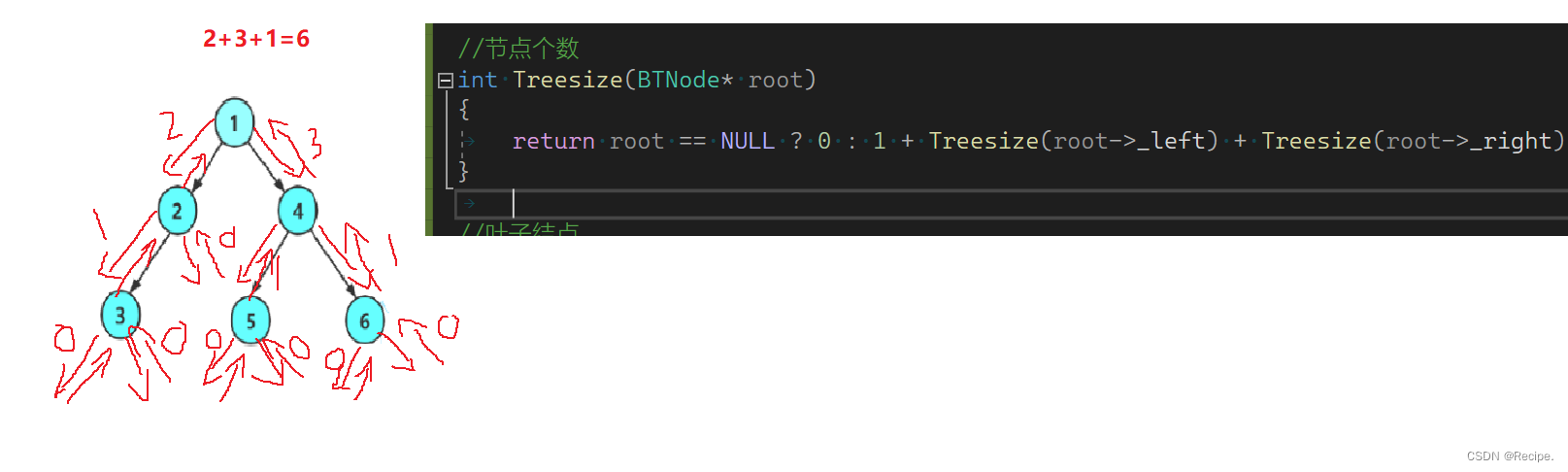
正确的求节点个数代码

//节点个数
int Treesize(BTNode* root)
{return root == NULL ? 0 : 1 + Treesize(root->_left) + Treesize(root->_right);
}

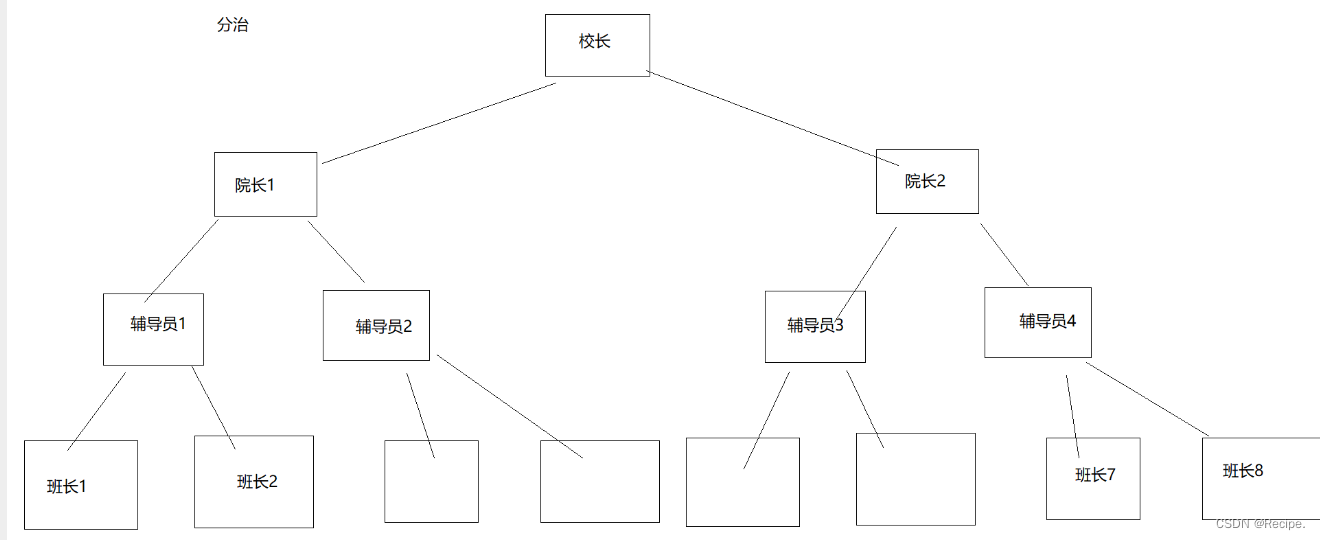
 思路：比如学校里面要统计在校人数，校长不可能一个个问每个人+1+1+1......，而是布置任务，给辅导员或者班主任，班主任或者辅导员会布置给班长去统计各班学生个数，班长汇报给辅导员或班主任，班主任或者辅导员汇报给校长，校长最后在汇报结果加上自己，就是学校在校总人数。

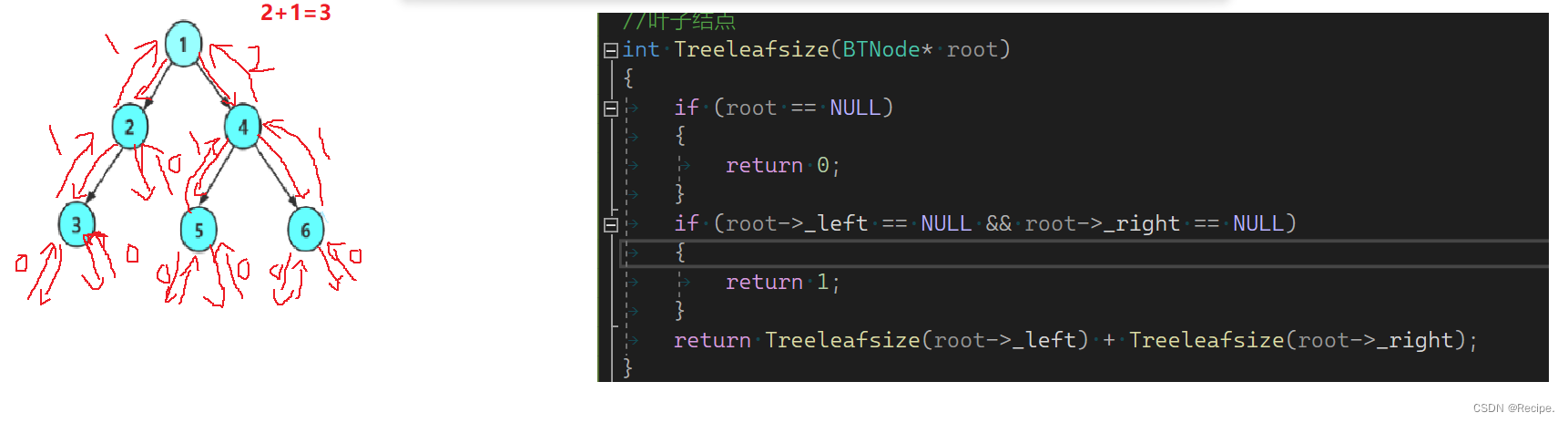
二叉树的叶子节点个数

叶子节点就是度为0的节点。

首先要判断根为不为空

再判断根节点的左右结点存不存在即可。

//叶子结点
int Treeleafsize(BTNode* root)
{if (root == NULL){return 0;}if (root->_left == NULL && root->_right == NULL){return 1;}return Treeleafsize(root->_left) + Treeleafsize(root->_right);
}

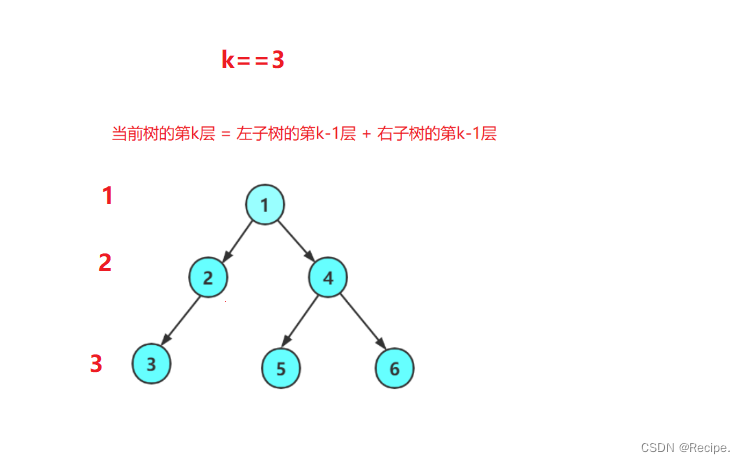
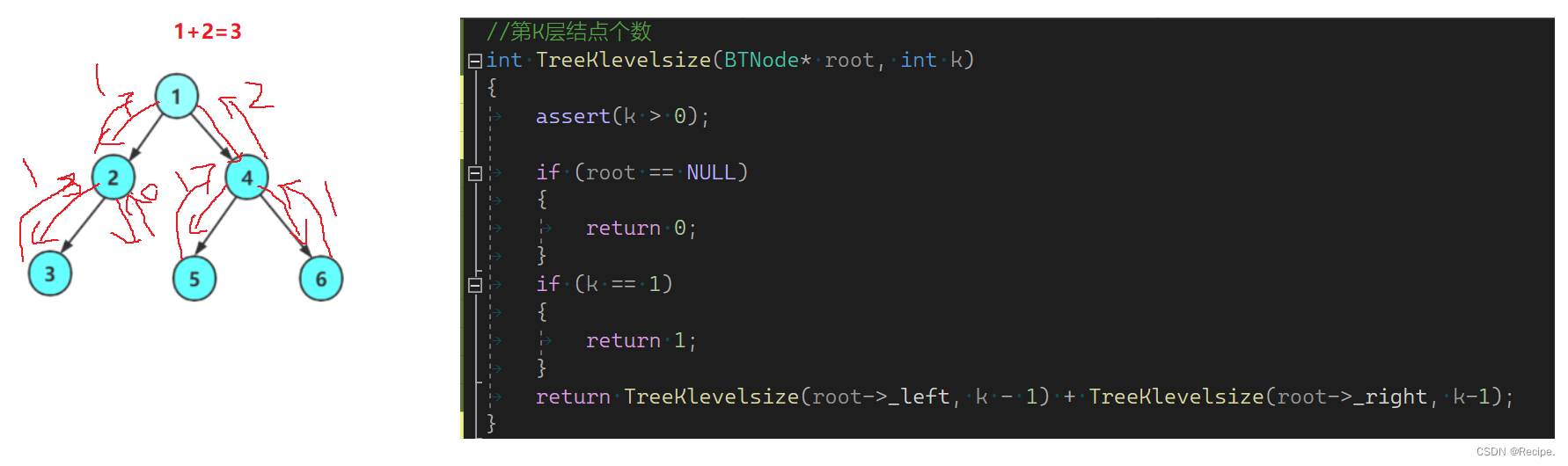
二叉树第k层的节点个数

//第K层结点个数
int TreeKlevelsize(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}return TreeKlevelsize(root->_left, k - 1) + TreeKlevelsize(root->_right, k-1);
}

 

完整代码

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<assert.h>
typedef struct BinaryTree
{struct BinaryTree* _left;struct BinaryTree* _right;int val;
}BTNode;BTNode* buynode(int x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->val = x;newnode->_left = NULL;newnode->_right = NULL;return newnode;
}void PreOrder(BTNode* root)
{if (root == NULL){printf(" NULL ");return;}printf("%d ", root->val);PreOrder(root->_left);PreOrder(root->_right);
}
void InOrder(BTNode* root)
{if (root == NULL){printf(" NULL ");return;}InOrder(root->_left);printf("%d ", root->val);InOrder(root->_right);
}
void PostOrder(BTNode* root)
{if (root == NULL){printf(" NULL ");return;}PostOrder(root->_left);PostOrder(root->_right);printf("%d ", root->val);
}//节点个数
int Treesize(BTNode* root)
{return root == NULL ? 0 : 1 + Treesize(root->_left) + Treesize(root->_right);
}//叶子结点
int Treeleafsize(BTNode* root)
{if (root == NULL){return 0;}if (root->_left == NULL && root->_right == NULL){return 1;}return Treeleafsize(root->_left) + Treeleafsize(root->_right);
}
//第K层结点个数
int TreeKlevelsize(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}return TreeKlevelsize(root->_left, k - 1) + TreeKlevelsize(root->_right, k-1);
}
int main()
{BTNode* newnode1 = buynode(1);BTNode* newnode2 = buynode(2);BTNode* newnode3 = buynode(3);BTNode* newnode4 = buynode(4);BTNode* newnode5 = buynode(5);BTNode* newnode6 = buynode(6);newnode1->_left = newnode2;newnode2->_left = newnode3;newnode1->_right = newnode4;newnode4->_left = newnode5;newnode4->_right = newnode6;PreOrder(newnode1);printf("\n");InOrder(newnode1);printf("\n");PostOrder(newnode1);printf("\n");printf("Treesize:%d\n", Treesize(newnode1));printf("Treeleafsize:%d\n", Treeleafsize(newnode1));printf(" TreeKlevelsize:%d\n", TreeKlevelsize(newnode1,3));return 0;
}