这么给网站做关键字域名查询网址
56. 合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]] 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
class Solution {
public:static bool cmp(const vector<int>& a,const vector<int>& b){return a[0] < b[0];}vector<vector<int>> merge(vector<vector<int>>& intervals) {vector<vector<int>> res; if(intervals.size() ==0) return res;sort(intervals.begin(),intervals.end(),cmp);res.push_back(intervals[0]);for(int i = 1; i < intervals.size(); i++){if(res.back()[1] >= intervals[i][0]){res.back()[1] = max(res.back()[1],intervals[i][1]);}else{res.push_back(intervals[i]);}}return res;}
};738. 单调递增的数字
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。
示例 1:
输入: n = 10 输出: 9
示例 2:
输入: n = 1234 输出: 1234
class Solution {
public:int monotoneIncreasingDigits(int n) {string nums =to_string(n);int idx = nums.size();for(int i = nums.size() - 1 ; i > 0 ; i--){if(nums[i - 1] > nums[i]){nums[i-1]--;//为什么需要使用--而不是nums[i-1] = nums[i] -1;idx = i;}}for(int i = idx ; i < nums.size(); i++){nums[i] = '9';}return stoi(nums);}
};968. 监控二叉树
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
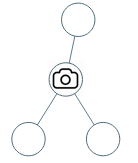
输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:int res;int traveltree(TreeNode* cur){if(cur == NULL) return 2;int left = traveltree(cur->left);int right = traveltree(cur->right);if(left == 2 && right == 2) return 0;if(left == 0 || right == 0){res++; return 1;}if(left == 1 || right == 1){return 2;}return -1;}public:int minCameraCover(TreeNode* root) {res = 0;if(traveltree(root) == 0) res++;return res;}
};