如何做旅游休闲网站百度首页百度一下

---

1.AVL树的概念

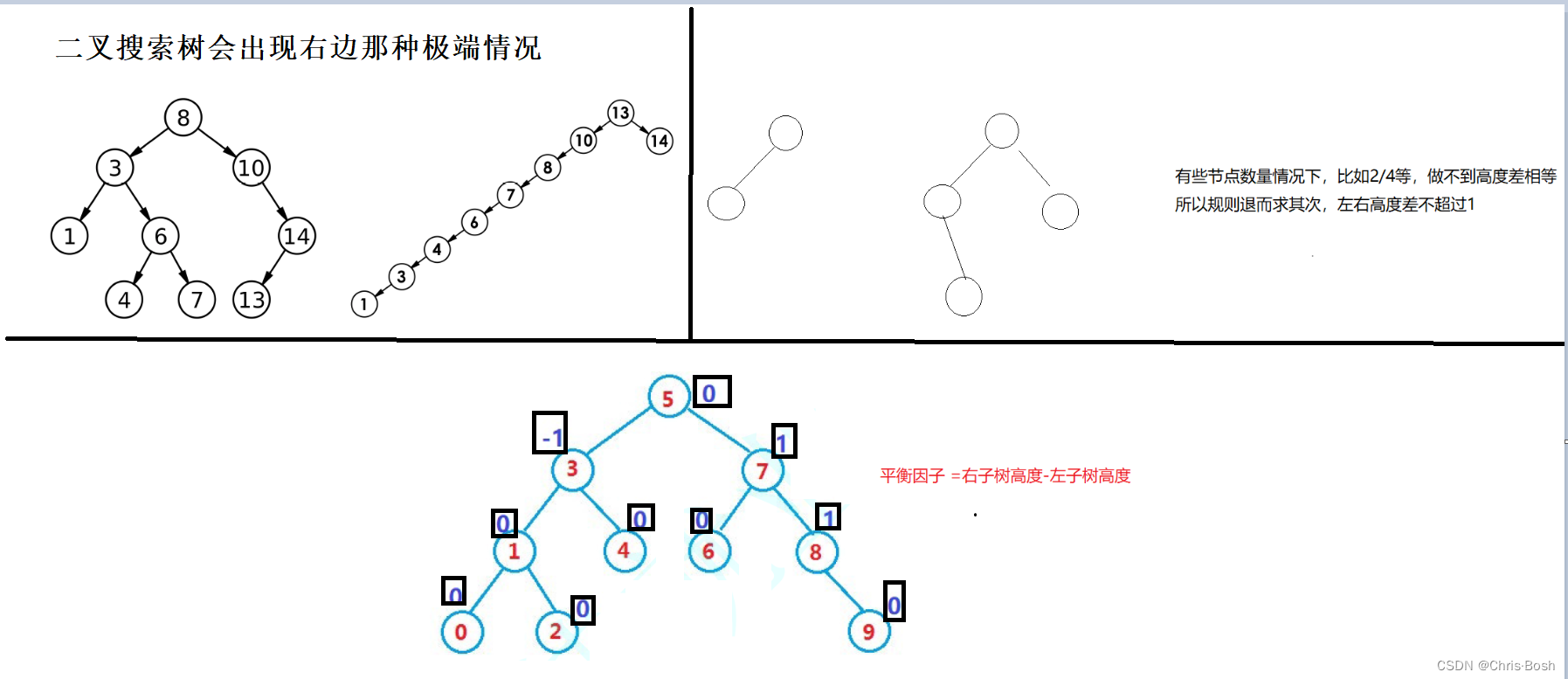
当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：
①它的左右子树都是AVL树
②左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

如果一棵二叉搜索树是高度平衡的，它就是AVL树。

2.AVL树的插入和旋转

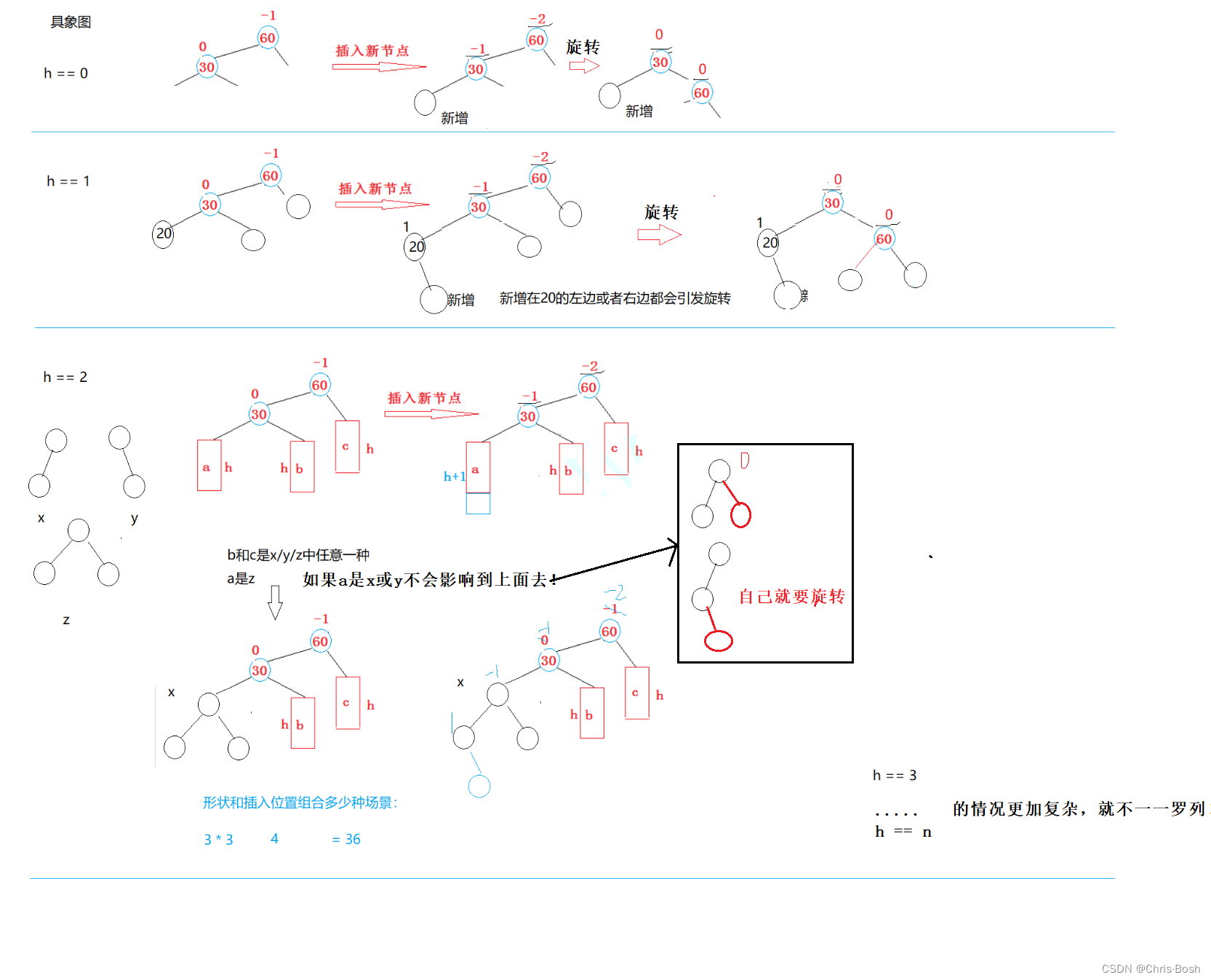
AVL树的插入：

3.AVL树的旋转

3.1旋转的底层：

以右旋转为例：

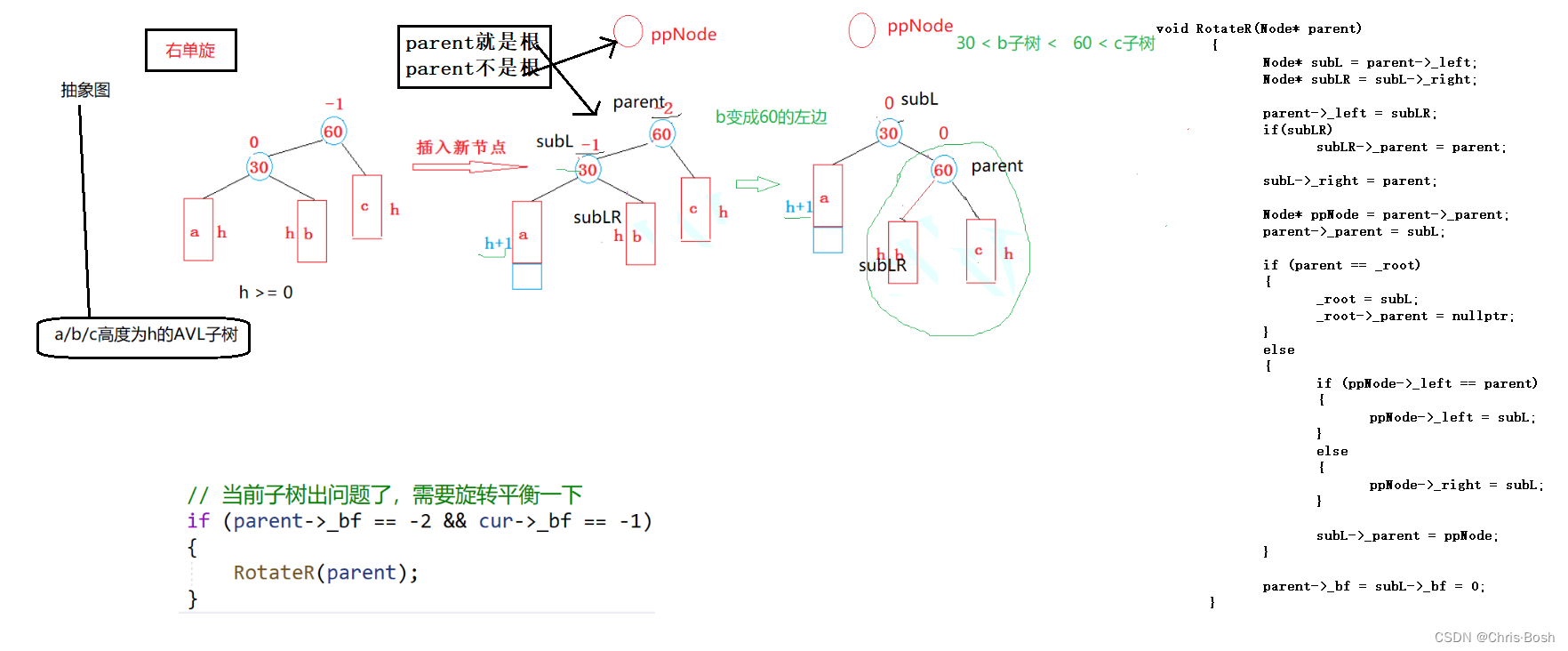
3.2 右旋转

3.3 左旋转

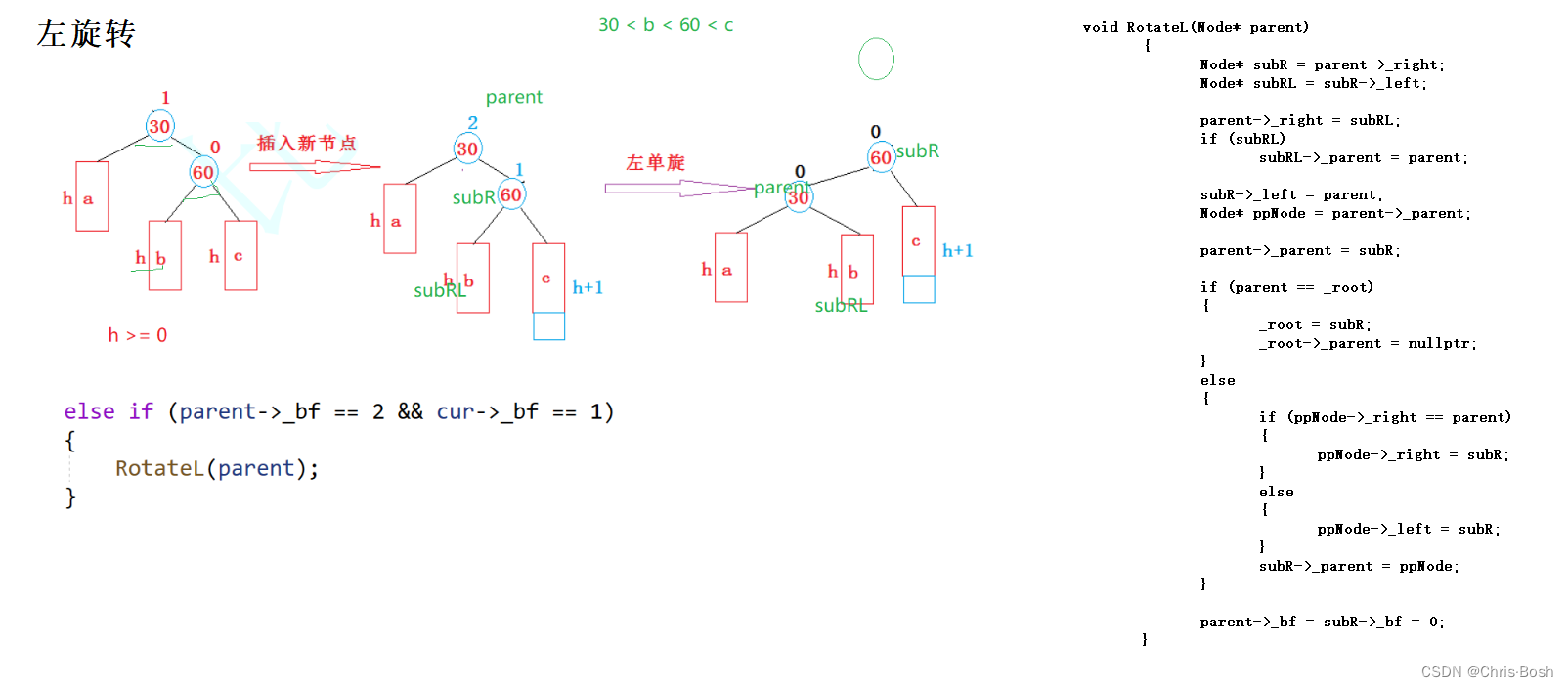
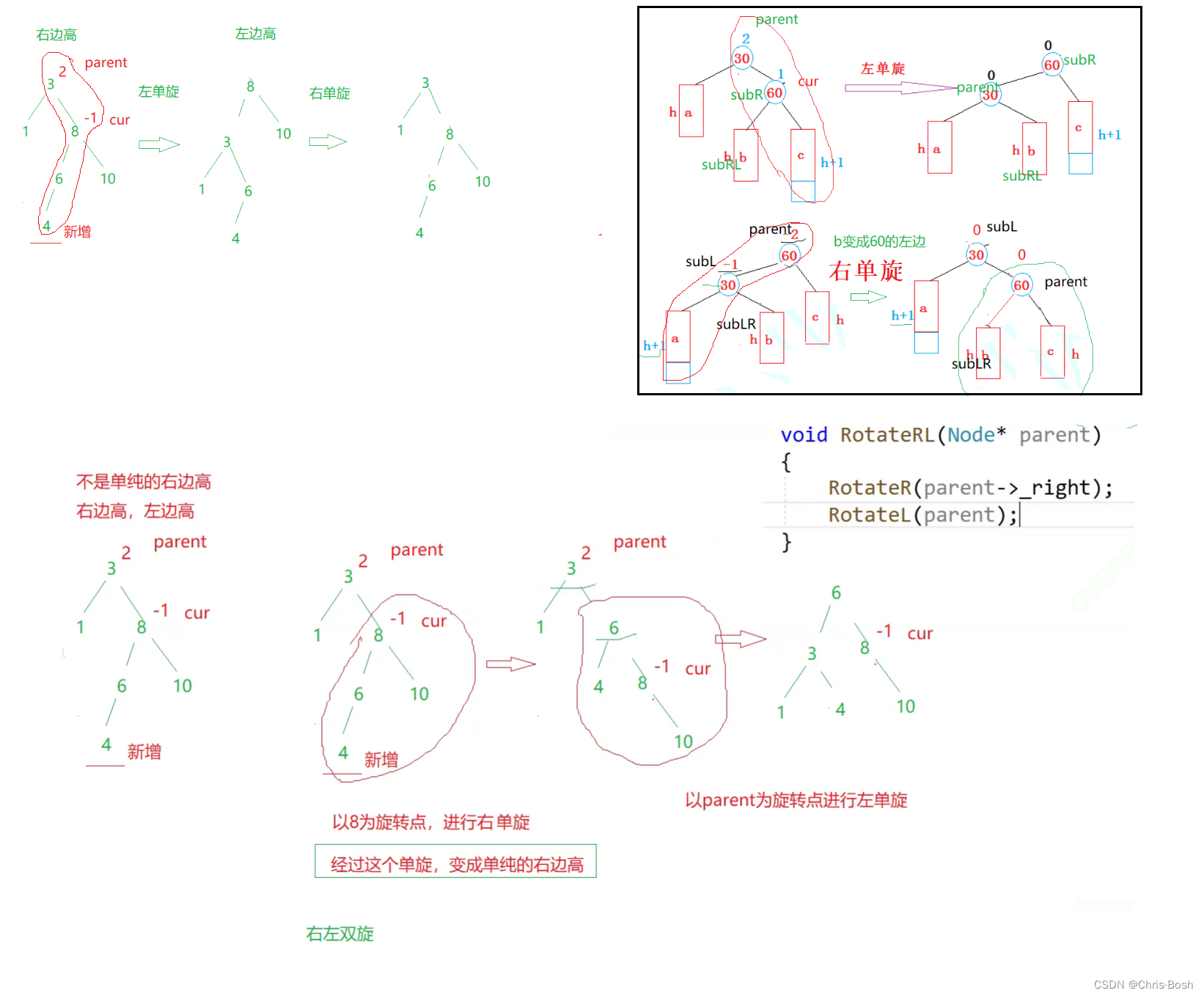
3.4 双旋

右左双旋：

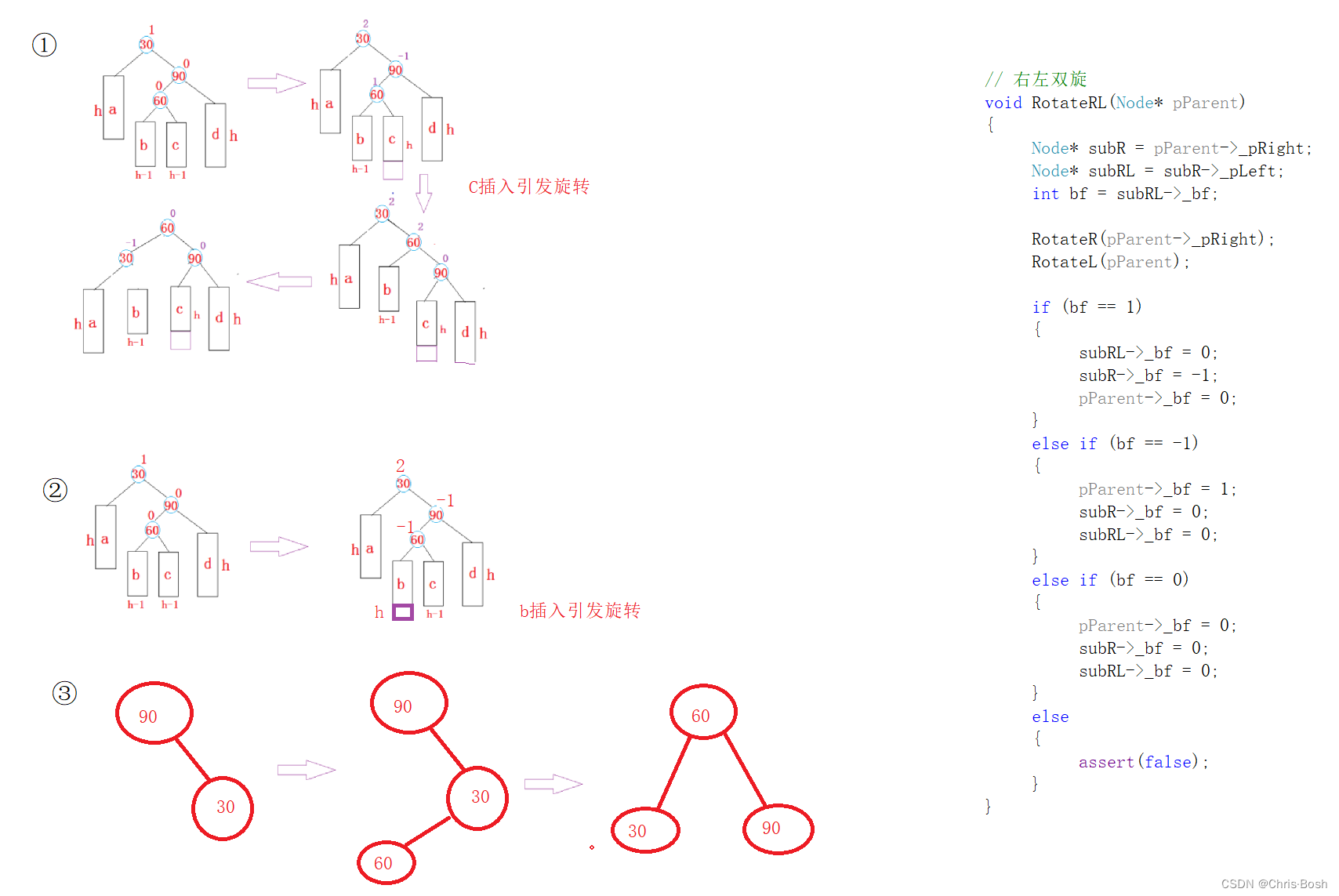
左右双旋：

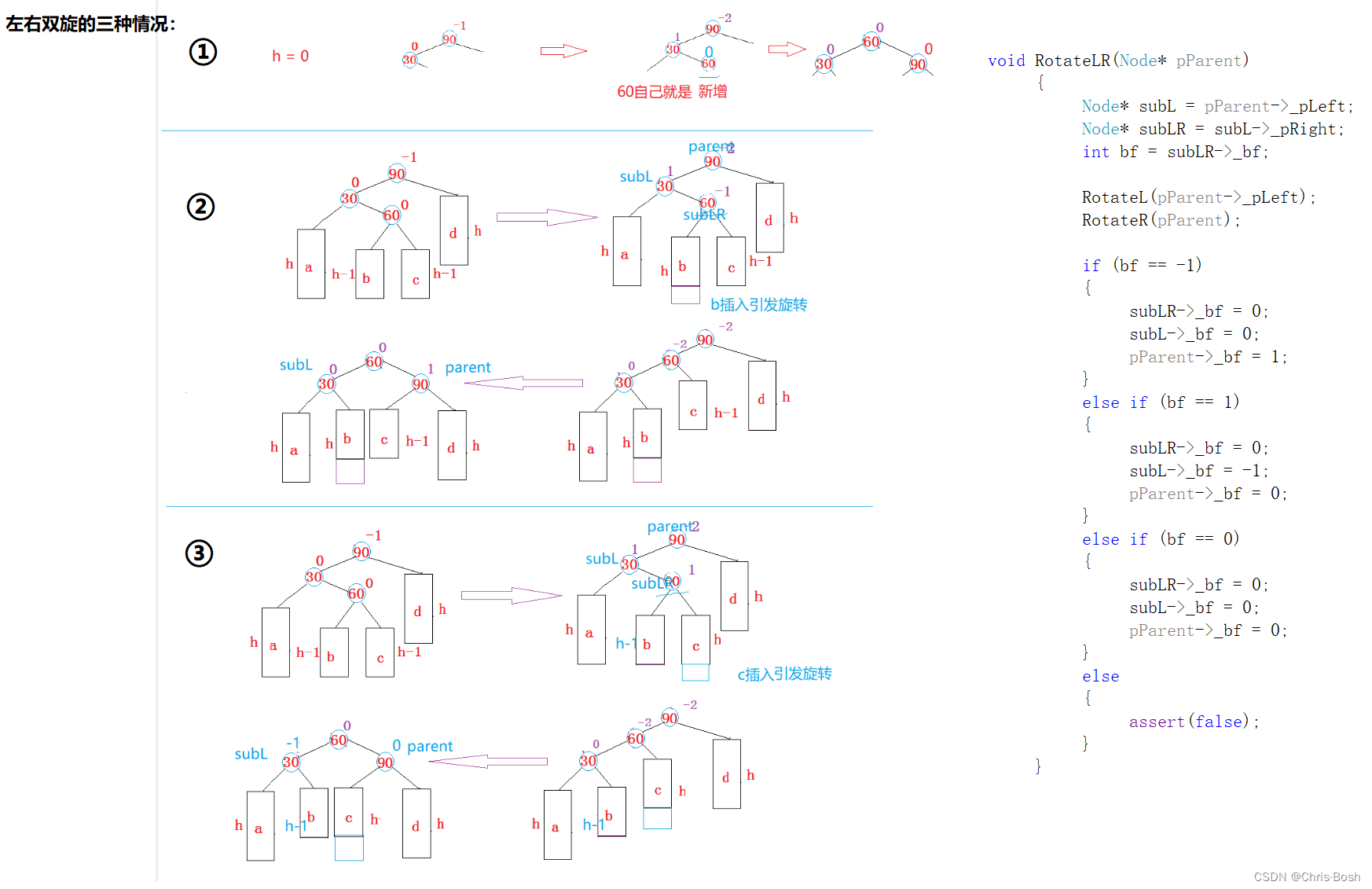
4.AVL树的底层

#pragma once
#include<assert.h>
#include<vector>
#include<iostream>
using namespace std;template<class T>
struct AVLTreeNode
{AVLTreeNode(const T& data = T()): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _pLeft;AVLTreeNode<T>* _pRight;AVLTreeNode<T>* _pParent;T _data;int _bf;   // 节点的平衡因子
};// AVL: 二叉搜索树 + 平衡因子的限制
template<class T>
class AVLTree
{typedef AVLTreeNode<T> Node;
public:AVLTree(): _pRoot(nullptr){}// 在AVL树中插入值为data的节点bool Insert(const T& data){if (_pRoot == nullptr){_pRoot = new Node(data);return true;}Node* parent = nullptr;Node* cur = _pRoot;while (cur != nullptr){if (cur->_data < data){parent = cur;cur = cur->_pRight;}else if (cur->_data > data){parent = cur;cur = cur->_pLeft;}else{return false;}}cur = new Node(data);if (parent->_data < data){parent->_pRight = cur;}else{parent->_pLeft = cur;}cur->_pParent = parent;// 更新平衡因子while (parent != nullptr){if (cur == parent->_pLeft){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_pParent;}else if (parent->_bf == -2 || parent->_bf == 2){// 当前子树出问题了，需要旋转平衡一下if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}break;}else{// 理论而言不可能出现这个情况assert(false);}}return true;}// AVL树的验证bool IsAVLTree(){return _IsAVLTree(_pRoot);}int Height(){return _Height(_pRoot);}int Size(){return _Size(_pRoot);}private:// 根据AVL树的概念验证pRoot是否为有效的AVL树bool _IsAVLTree(Node* pRoot){if (pRoot == nullptr){return true;}int leftHeight = _Height(pRoot->_pLeft);int rightHeight = _Height(pRoot->_pRight);// 不平衡if (abs(leftHeight - rightHeight) >= 2){std::cout << pRoot->_data << std::endl;return false;}//检查一下平衡因子是否正确if (rightHeight - leftHeight != pRoot->_bf){cout << pRoot->_data << endl;return false;}return _IsAVLTree(pRoot->_pLeft) && _IsAVLTree(pRoot->_pRight);}size_t _Height(Node* pRoot){if (pRoot == nullptr)return 0;return max(_Height(pRoot->_pLeft), _Height(pRoot->_pRight)) + 1;}// 右单旋void RotateR(Node* pParent){Node* subL = pParent->_pLeft;Node* subLR = subL->_pRight;pParent->_pLeft = subLR;if (subLR != nullptr){subLR->_pParent = pParent;}subL->_pRight = pParent;Node* ppNode = pParent->_pParent;pParent->_pParent = subL;if (pParent == _pRoot){_pRoot = subL;_pRoot->_pParent = nullptr;}else{if (ppNode->_pLeft == pParent){ppNode->_pLeft = subL;}else{ppNode->_pRight = subL;}subL->_pParent = ppNode;}pParent->_bf = subL->_bf = 0;}// 左单旋void RotateL(Node* pParent){Node* subR = pParent->_pRight;Node* subRL = subR->_pLeft;pParent->_pRight = subRL;if (subRL != nullptr){subRL->_pParent = pParent;}subR->_pLeft = pParent;Node* ppNode = pParent->_pParent;pParent->_pParent = subR;if (pParent == _pRoot){_pRoot = subR;_pRoot->_pParent = nullptr;}else{if (ppNode->_pRight == pParent){ppNode->_pRight = subR;}else{ppNode->_pLeft = subR;}subR->_pParent = ppNode;}pParent->_bf = subR->_bf = 0;}// 右左双旋void RotateRL(Node* pParent){Node* subR = pParent->_pRight;Node* subRL = subR->_pLeft;int bf = subRL->_bf;RotateR(pParent->_pRight);RotateL(pParent);if (bf == 1){subRL->_bf = 0;subR->_bf = -1;pParent->_bf = 0;}else if (bf == -1){pParent->_bf = 1;subR->_bf = 0;subRL->_bf = 0;}else if (bf == 0){pParent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else{assert(false);}}// 左右双旋void RotateLR(Node* pParent){Node* subL = pParent->_pLeft;Node* subLR = subL->_pRight;int bf = subLR->_bf;RotateL(pParent->_pLeft);RotateR(pParent);if (bf == -1){subLR->_bf = 0;subL->_bf = 0;pParent->_bf = 1;}else if (bf == 1){subLR->_bf = 0;subL->_bf = -1;pParent->_bf = 0;}else if (bf == 0){subLR->_bf = 0;subL->_bf = 0;pParent->_bf = 0;}else{assert(false);}}private:Node* _pRoot;
};void TestAVLTree1()
{//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };AVLTree<int> t1;for (auto e : a){// 1、先看是插入谁导致出现的问题// 2、打条件断点，画出插入前的树// 3、单步跟踪，对比图一一分析细节原因t1.Insert({ e});cout << "Insert:" << e << "->" << t1.IsAVLTree() << endl;}cout << t1.IsAVLTree() << endl;
}