资源网站的建设搜索引擎推广简称
从0开始的秋招刷题路,记录下所刷每道题的题解,帮助自己回顾总结
802. 找到最终的安全状态
有一个有 n 个节点的有向图,节点按 0 到 n - 1 编号。图由一个 索引从 0 开始 的 2D 整数数组 graph表示, graph[i]是与节点 i 相邻的节点的整数数组,这意味着从节点 i 到 graph[i]中的每个节点都有一条边。
如果一个节点没有连出的有向边,则它是 终端节点 。如果没有出边,则节点为终端节点。如果从该节点开始的所有可能路径都通向 终端节点 ,则该节点为 安全节点 。
返回一个由图中所有 安全节点 组成的数组作为答案。答案数组中的元素应当按 升序 排列。
示例 1:
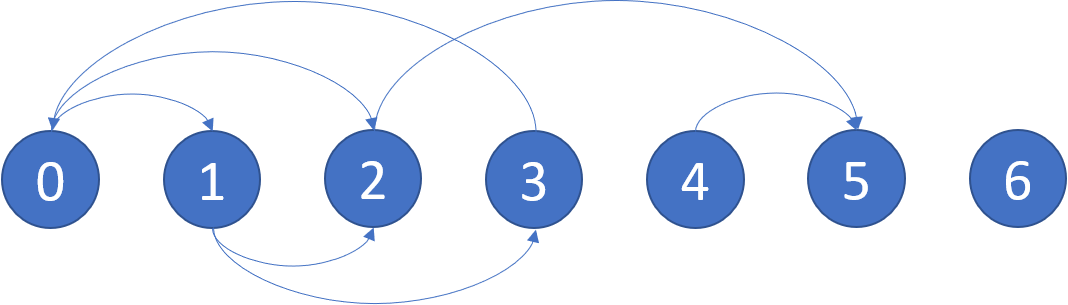
输入:graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出:[2,4,5,6]
解释:示意图如上。
节点 5 和节点 6 是终端节点,因为它们都没有出边。
从节点 2、4、5 和 6 开始的所有路径都指向节点 5 或 6 。
示例 2:
输入:graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
输出:[4]
解释:
只有节点 4 是终端节点,从节点 4 开始的所有路径都通向节点 4 。
提示:
n == graph.length
1 <= n <= 1 0 4 10^4 104
0 <= graph[i].length <= n
0 <= graph[i][j] <= n - 1
graph[i] 按严格递增顺序排列。
图中可能包含自环。
图中边的数目在范围 [1, 4 ∗ 1 0 4 4 * 10^4 4∗104] 内。
解题思路
拓扑的解法中,所有出度为0的点是安全的,那么出到这些点的点也可以减去这条边,如果其剩下的出度为0,它也是安全的,以此类推。
搜索的时候可以标记节点的当前状态,如果他有出口,暂定为1,如果他的出口全部为安全的点,他们的和必然为0,就认定它也是安全的,否则它是不安全的。
代码
拓扑
class Solution {public List<Integer> eventualSafeNodes(int[][] graph) {int n = graph.length;int[] out = new int[n];Map<Integer, List<Integer>> edges = new HashMap<>();for(int i=0;i<n;i++)for(int j:graph[i]){List<Integer> cur = edges.getOrDefault(j, new ArrayList<>());cur.add(i);edges.put(j, cur);out[i]++;}Deque<Integer> queue = new LinkedList<>();for(int i=0;i<n;i++)if(out[i]==0)queue.add(i);List<Integer> ans = new ArrayList<>();while(queue.size()>0){int node = queue.pollFirst();ans.add(node);if(edges.containsKey(node))for(int nxt: edges.get(node)){out[nxt]--;if(out[nxt] == 0)queue.add(nxt);}}Collections.sort(ans);return ans;}
}
DFS
class Solution {int[][] graph_;int[] states;public List<Integer> eventualSafeNodes(int[][] graph) {int n = graph.length;// 每个点可能的状态: -1:点是未走过的, 0:点是安全的,1:点是走过的不确定安不安全,2:点是不安全的states = new int[n];Arrays.fill(states, -1);graph_ = graph;List<Integer> ans = new ArrayList<>();for(int i=0;i<n;i++)if(dfs(i)==0)ans.add(i);return ans;}public int dfs(int node){if(states[node] == -1){states[node] = 1;for(int nxt:graph_[node]){states[node] += dfs(nxt);if(states[node] > 1)break;}if(states[node] == 1)states[node] = 0;elsestates[node] = 2;}return states[node];}
}
DFS也可以使用纯boolean来标记
class Solution {int[][] graph_;Map<Integer,Boolean> states;public List<Integer> eventualSafeNodes(int[][] graph) {int n = graph.length;graph_ = graph;states = new HashMap<>();List<Integer> ans = new ArrayList<>();for(int i=0;i<n;i++){if(safe(i))ans.add(i);}return ans;}public boolean safe(int node){if(!states.containsKey(node)){states.put(node, false);boolean allTrue = true;for(int nxt: graph_[node])if(!safe(nxt)){allTrue = false;break;}states.put(node, allTrue);}return states.get(node);}
}
