怎么查询公司名字是否被注册武汉网站建设方案优化

 目录

前言

生成树

1.基本概念

 2.生成树的特点

 3.生成树形成过程

最小生成树(Minimum Spanning Tree)

1.基本概念

2.构造方法（MST）

普里姆(Prime)算法

1.算法思想

2.代码实现

克鲁斯卡尔（Kruskal）算法

1.算法思想

 2.代码实现

Prime算法与Kruskal算法比较

---

前言

        今天我们学习图的应用，对于最小生成树问题，那什么是最小生成树呢？图又这么去实现一个生成树和最小生成树？下面我们就一起来看看。

生成树

1.基本概念

生成树:所有顶点均由边连接在一起，但不存在回路的图。

 如上图所示，除了第一个不是生成树（因为存在环），其他都是生成树。

 2.生成树的特点

图的生成树有以下特点：

• 一个图可以有许多棵不同的生成树
• 生成树的顶点个数与图的顶点个数相同
• 生成树是图的极小连通子图，去掉一条边则非连通
• 一个有n个顶点的连通图的生成树有n-1条边
• 在生成树中再加一条边必然形成回路。
• 生成树中任意两个顶点间的路径是唯一的

 3.生成树形成过程

形成过程：

设图G=(V,E)是个连通图，当从图任一顶点出发遍历图G时，将边集E(G)分成两个集合T(G)和B(G)。其中T(G)是遍历图时所经过的边的集合，B(G)是遍历图时未经过的边的集合。显然，G1(V,T)是图G的极小连通子图。即子图G1是连通图G的生成树。

最小生成树(Minimum Spanning Tree)

1.基本概念

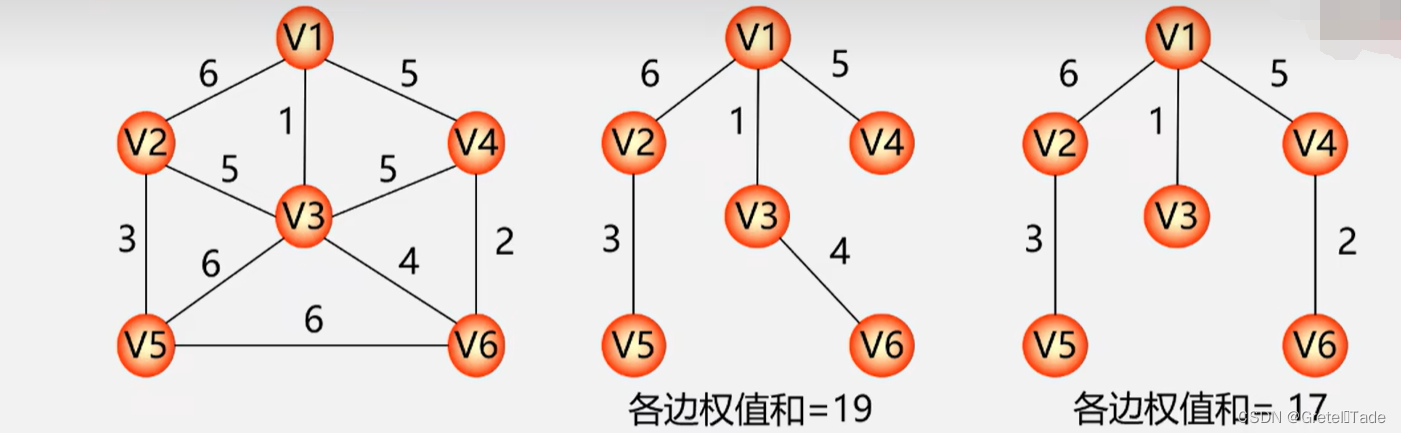
最小生成树:给定一个无向网络，在该网的所有生成树中，使得各边权值之和最小的那棵生成树称为该网的最小生成树，也叫最小代价生成树。

如图所示，连通图的最小生成树权值之和为17才是最小生成树

2.构造方法（MST）

最小生成树（Minimum Spanning Tree），根据其英文名字有一个叫MST算法用于去构造最小生成树，MST算法本质是一种贪心算法，根据贪心算法的方式去获取到最优解。

 MST 性质:设N= (V,E)是一个连通网，U是顶点集V的一个非空子集。若边(u, v)是一条具有最小权值的边，其中uEu,vEV-U，则必存在一棵包含边(u, v)的最小生成树。

MST解释说明：

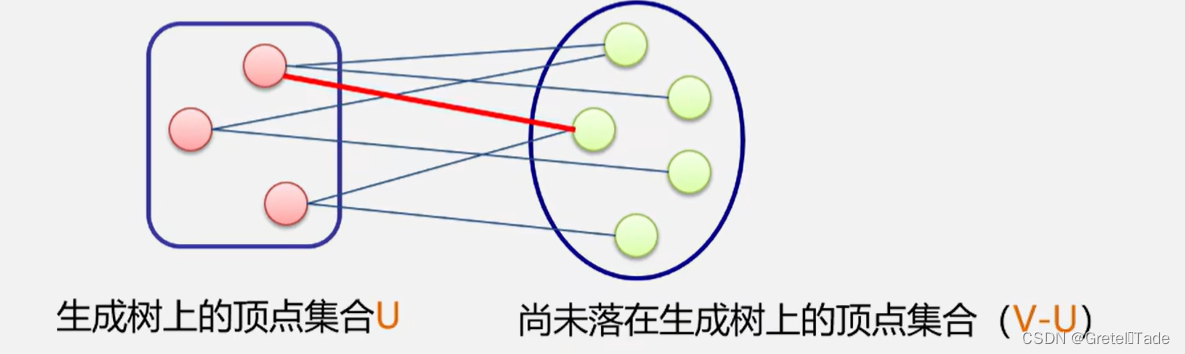
在生成树的构造过程中，图中n个顶点分属两个集合: 

• 已落在生成树上的顶点集:u ·已落在生成树上的顶点集：U
• 尚未落在生成树上的顶点集:V-U ·尚未落在生成树上的顶点集：V-U

接下来则应在所有连通U中顶点和V-U中顶点的边中选取权值最小的边 接下来则应在所有连通U中顶点和V-U中顶点的边中选取权值最小的边

下面我就介绍两种MST算法，分别是Prim算法和Kruskal算法。

以下代码是一个图的邻接矩阵创建代码：

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define Maxint 32767
#define Maxnum 100//最大顶点数//数据类型
typedef struct d {char id[10];//……
}
ElemType;
//图的邻接数组
typedef struct graph {ElemType vexs[Maxnum];//图数据int matrix[Maxnum][Maxnum];//二维数组int vexnum;//点数int arcnum;//边数
}Graph;//节点id查找下标
int Locate_vex(Graph G, char* id) {for (int i = 0; i < G.vexnum; i++)if (strcmp(G.vexs[i].id, id) == 0)return i;return -1;
}//构造邻接矩阵(无向图，对称矩阵)(有向图)赋权图
void Create_graph(Graph* G) {printf("请输入顶点个数和边的个数：\n");scanf("%d %d", &G->vexnum, &G->arcnum);//输入点数边数printf("请输入顶点数据:\n");for (int i = 0; i < G->vexnum; i++) {scanf("%s", G->vexs[i].id);}for (int x = 0; x < G->vexnum; x++) {for (int y = 0; y < G->vexnum; y++) {if (x == y)G->matrix[x][y] = 0;//对角线初始化为0elseG->matrix[x][y] = Maxint;//其他初始化为Maxint}}printf("请输入边相关数据:\n");for (int k = 0; k < G->arcnum; k++) {char a[10], b[10];int w;scanf("%s %s %d", a, b, &w);//a->bint i = Locate_vex(*G, a);int j = Locate_vex(*G, b);//矩阵赋值G->matrix[i][j] = w;G->matrix[j][i] = w;//删掉这个，表示有向图}
}//输出矩阵
void print_matrix(Graph G) {printf("矩阵为：\n");for (int i = 0; i < G.vexnum; i++) {for (int j = 0; j < G.vexnum; j++) {if(G.matrix[i][j]==Maxint)printf("∞\t");elseprintf("%d\t", G.matrix[i][j]);}printf("\n");}printf("图的顶点个数和边数：%d,%d\n", G.vexnum, G.arcnum);
}//遍历
void visit(Graph G, int loca) {printf("%s ", G.vexs[loca].id);
}

普里姆(Prime)算法

1.算法思想

Prime算法的核心步骤是：在带权连通图中V是包含所有顶点的集合， U已经在最小生成树中的节点，从图中任意某一顶点v开始，此时集合U={v}，重复执行下述操作：在所有u∈U,w∈V-U的边(u,w)∈E中找到一条权值最小的边，将(u,w)这条边加入到已找到边的集合，并且将点w加入到集合U中，当U=V时，就找到了这颗最小生成树

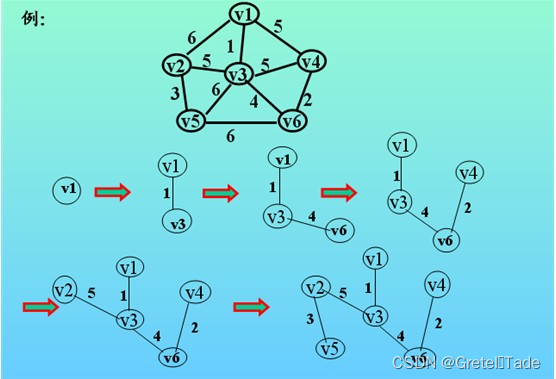
        其实，算法的核心步骤就是：在所有u∈U,w∈V-U的边(u,w)∈E中找到一条权值最小的边。

过程如下图所示：

2.代码实现

							//最小生成树
//生成树
typedef struct shortedge {char adjvex_id[10];//储存到的数据idint lowcost;//到其他顶点最短路径距离
}ShortEdge;
//01---Prim算法							
//在U集合中找到距离其他顶点最近的下一个顶点位置
int min_path(Graph G, ShortEdge* shortedge) {int  location;int min = Maxint;for (int i = 1; i < G.vexnum; i++) {if (min > shortedge[i].lowcost && shortedge[i].lowcost != 0) {min = shortedge[i].lowcost;location = i;}}return location;
}
//Prim接口
void MST_Prim(Graph G, char* start) {printf("(Prim)最小生成树如下：\n");ShortEdge shortdege[Maxnum];//集合Uint sum = 0;//统计最短路径权之和//对第一个起始数据start初始化处理，把第一个顶点放入到集合U当中int k = Locate_vex(G, start);//当前集合U只有顶点start，那么里面的数据就储存start的数据for (int i = 0; i < G.vexnum; i++) {strcpy(shortdege[i].adjvex_id, start);shortdege[i].lowcost = G.matrix[k][i];}shortdege[k].lowcost = 0;//此顶点对应的下标标记为0，表示已经加入集合U当中//后继处理for (int i = 0; i < G.vexnum-1; i++) {//找到下一个离集合U最近的顶点，下标为kk = min_path(G, shortdege);sum += shortdege[k].lowcost;printf("%s->%s %d\n", shortdege[k].adjvex_id, G.vexs[k].id, shortdege[k].lowcost);shortdege[k].lowcost = 0;//此顶点对应的下标标记为0，表示已经加入集合U当中//加入了新的顶点后，对集合U到其他顶点最近距离的值进行更新for (int j = 0; j < G.vexnum; j++) {if (G.matrix[k][j] < shortdege[j].lowcost && shortdege[j].lowcost!=0) {shortdege[j].lowcost = G.matrix[k][j];strcpy(shortdege[j].adjvex_id, G.vexs[k].id);}}}printf("最小生成树权之和为：%d\n", sum);
}

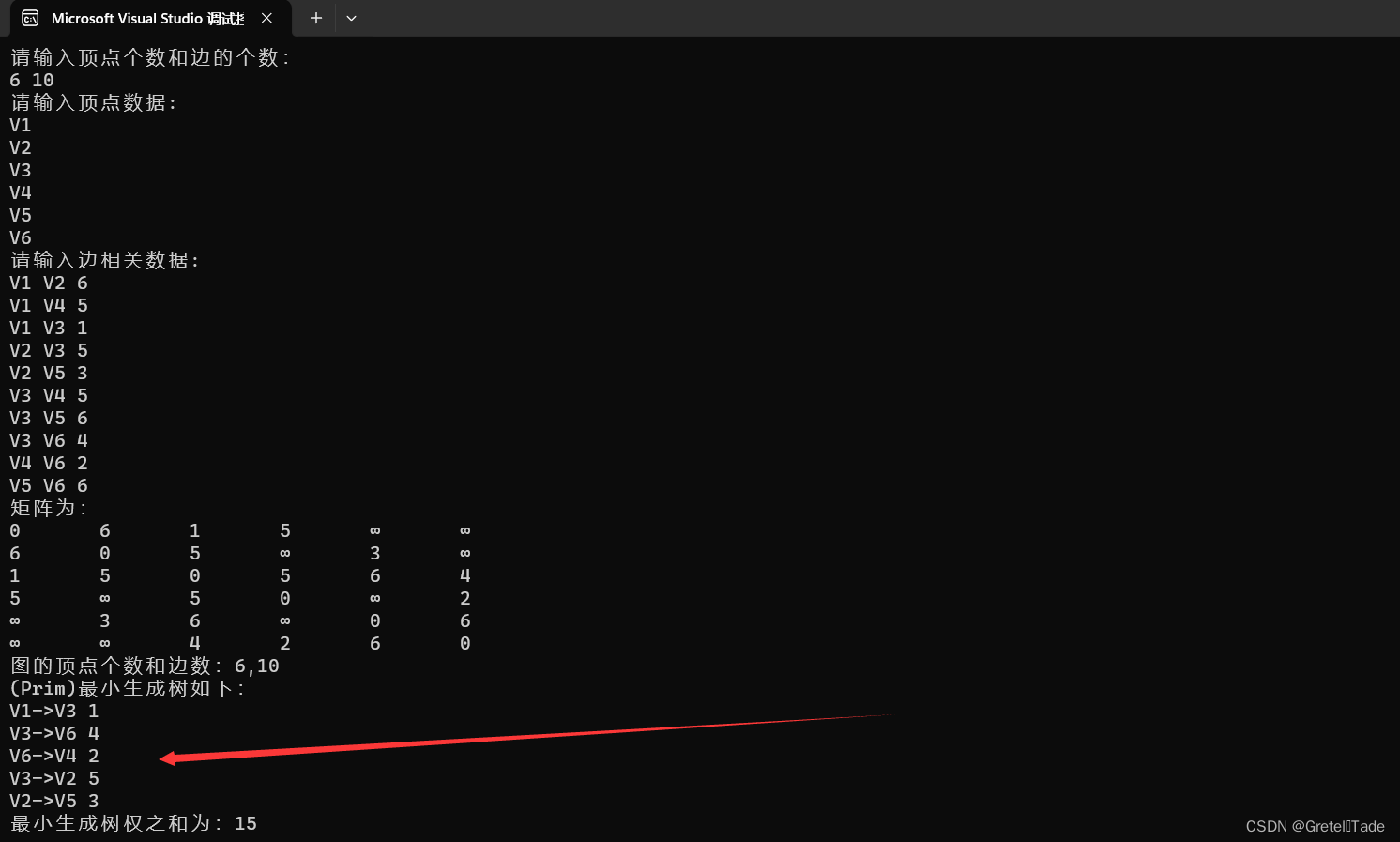
 测试结果：

int main() {Graph G;Create_graph(&G);print_matrix(G);MST_Prim(G, "V1");
}

克鲁斯卡尔（Kruskal）算法

1.算法思想

克鲁斯卡尔算法是一种用于求解最小生成树问题的贪心算法。 最小生成树是一个连通图的生成树，其边的权重之和最小。 一、原理 克鲁斯卡尔算法的核心思想是按照边的权重从小到大逐渐选择连通图的边，直到所有顶点都被连接为止。 在每一步中，选择当前权重最小的边，若该边的两个顶点尚未连接，则将其添加到最小生成树的边集合中，并将这两个顶点归为同一个连通分量。克鲁斯卡尔（Kruskal）算法又称作为避圈法。

过程如下：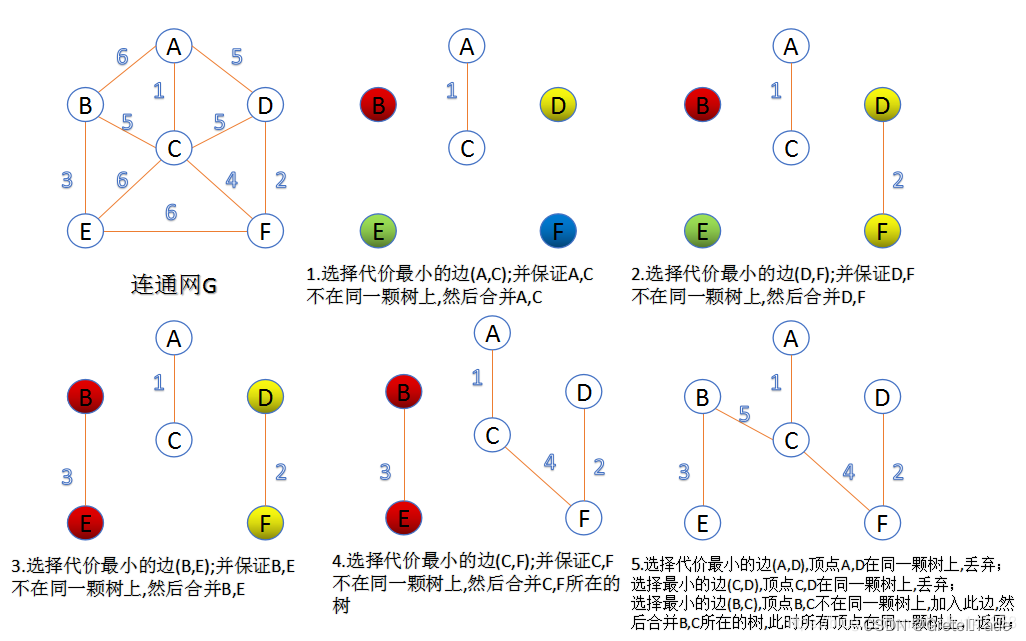

 2.代码实现

这里就需要对边进行权值的大小排序，直接就用快速排序去进行排序，（头文件.h）如下:

#pragma once
//边的结构体数据
typedef struct edge {char begin_id[10];//边起点的idchar end_id[10];//边终点的idint weight;//权值
}Edge;
void quick_sort(Edge* n, int left, int right);

快速排序源文件.c代码如下：

#include"sort.h"
//快速排序---递归实现
void quick_sort(Edge* n, int left, int right) {int i, j, temp;i = left;j = right;if (i > j) {return;}else {temp = n[left].weight;while (i != j) {while (n[j].weight >= temp && i < j)//先向左移动jj--;while (n[i].weight <= temp && i < j) //再向右移动ii++;if (i < j) {//此时对i和j指向的数字进行数字交换Edge num = n[i];n[i] = n[j];n[j] = num;}}//当i和j相遇的时候就结束循环//此时i与j相遇，就与temp交换Edge new_temp = n[i];n[i] = n[left];n[left] = new_temp;}//最后左右边依次进入到递归quick_sort(n, left, i - 1); //左边的数字都比temp要小quick_sort(n, i + 1, right);  //右边的数字都比temp要大
}

克鲁斯卡尔（Kruskal）算法代码如下：

						//最小生成树//02--Kruskal算法
//对边排序
Edge* arc_sort(Graph G) {//创建边数据Edge* edge = (int*)malloc(sizeof(Edge) * G.arcnum);int count = 0;//把边的数据储存到edge里面（无向图）for (int i = 0; i < G.vexnum; i++) {for (int j = 0; j <= i; j++) {if (G.matrix[i][j] != Maxint && G.matrix[i][j] != 0) {strcpy(edge[count].begin_id, G.vexs[i].id);strcpy(edge[count].end_id, G.vexs[j].id);edge[count].weight = G.matrix[i][j];count++;}}}//对边的权值进行排序quick_sort(edge, 0, count - 1);return edge;
}//接口
void MST_Kruskal(Graph G) {Edge* edge = arc_sort(G);int sum = 0;int vset[Maxnum];//辅助数组判断连通性//初始化为01234……表示开始的时候都不连通for (int i = 0; i < G.vexnum; i++)vset[i] = i;for (int i = 0; i < G.arcnum; i++) {int a = Locate_vex(G, edge[i].begin_id);//a为起点顶点的位置下标int b = Locate_vex(G, edge[i].end_id);//b为这个边终点的位置下标int v1 = vset[a];//辅助数组中找到起点的连通标准int v2 = vset[b];//辅助数组中找到终点的连通标准//判断v1与v2是否相等，判定是否成环if (v1!=v2) {printf("%s——%s %d\n", edge[i].begin_id, edge[i].end_id, edge[i].weight);sum += edge[i].weight;for (int j = 0; j < G.vexnum; j++) {//与v1连通的数据全部改成v2，表示整体连通if (vset[j] == v1)vset[j] = v2;}}}printf("最小生成树的权值之和：%d\n", sum);//释放空间free(edge);edge = NULL;
}

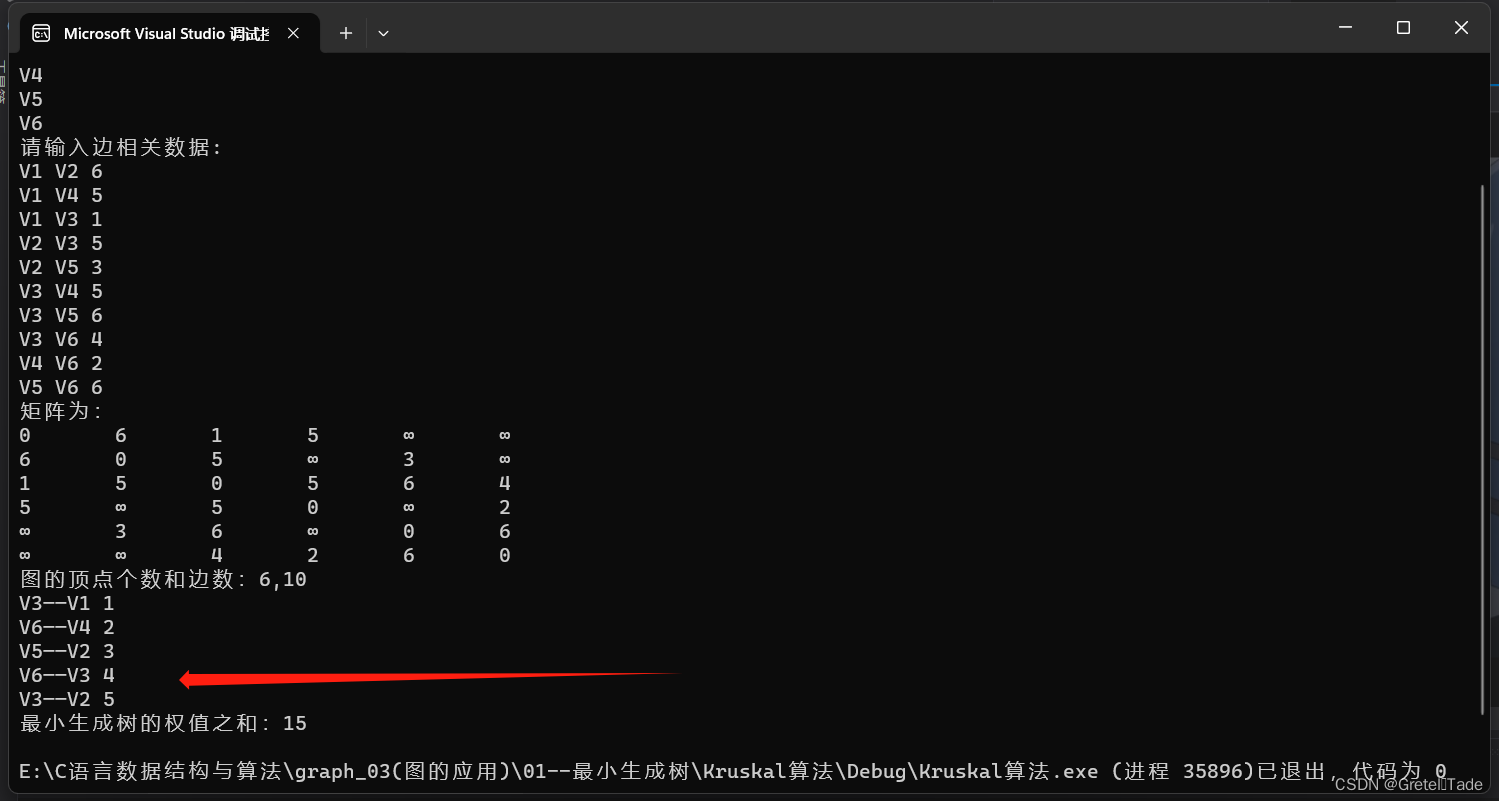
测试结果： 

int main() {Graph G;Create_graph(&G);print_matrix(G);MST_Kruskal(G);
}

Prime算法与Kruskal算法比较

 

以上就是本期的全部内容了，我们下一次见！

分享一张壁纸：