做网站需要每年都缴费吗电子商务营销的概念

一、题目描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

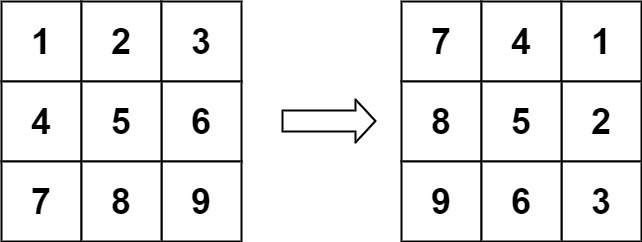
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

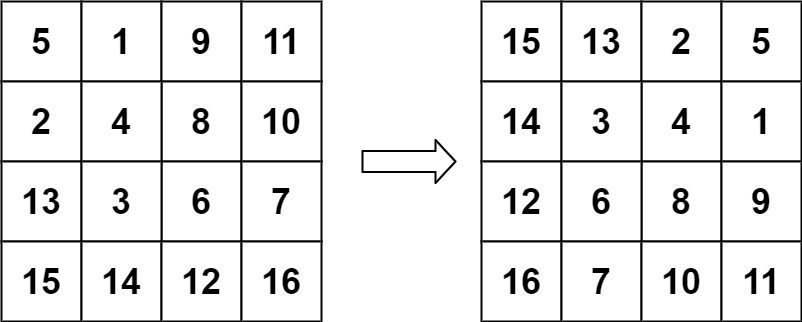
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

二、解题思路

1. 层次遍历：首先，我们可以观察到旋转操作实际上是将矩阵的每一层（从外到内）进行了交换。最外层的元素移动到了最底部，最底部的元素移动到了最右侧，最右侧的元素移动到了最顶部，最顶部的元素移动到了最左侧。因此，我们可以先对矩阵的最外层进行操作。

2. 保存最外层元素：在进行交换之前，我们需要保存最外层的元素，因为在旋转过程中，这些元素将被覆盖。

3. 交换元素：对于矩阵的每一层，我们需要将四个边界的元素进行交换。具体来说，对于每个元素位于最外层的 (i, j)，我们执行以下操作：

• 保存 matrix[i][j] 的值。
• 将 matrix[j][n-1-i]（最底部的元素）赋值给 matrix[i][j]。
• 将保存的值（原 matrix[i][j] 的值）赋值给 matrix[n-1-i][n-1-j]（最右侧的元素）。
• 以此类推，完成所有层次的旋转。

4. 逐层处理：从最外层开始，逐层向内处理，直到处理到矩阵的中心。

三、具体代码

class Solution {public void rotate(int[][] matrix) {int n = matrix.length; // 矩阵的大小 n x nint layers = n / 2; // 计算需要处理的层数for (int layer = 0; layer < layers; layer++) {int first = layer;int last = n - 1 - layer;for (int i = first; i < last; i++) {int offset = i - first;int top = matrix[first][i]; // 保存最上面的元素// 从左到右的元素依次交换matrix[first][i] = matrix[last - offset][first];matrix[last - offset][first] = matrix[last][last - offset];matrix[last][last - offset] = matrix[i][last];matrix[i][last] = top; // 恢复最上面的元素}}}
}

四、时间复杂度和空间复杂度

1. 时间复杂度

• 该算法主要包含一个外层循环，它遍历了矩阵的层数，这个层数是 n/2，其中 n 是矩阵的大小。
• 对于每个层，我们进行了一个内层循环，这个循环遍历了每一层的元素。内层循环的次数是 (last - first)，这个值随着层数的增加而减少，但总体上可以认为是 n。
• 因此，总的时间复杂度是 O(n)，因为每个元素都被访问和修改了一次。

2. 空间复杂度

• 该算法没有使用任何额外的数据结构来存储矩阵的元素，所有的操作都是在原地进行的。
• 我们只使用了少量的变量来保存在交换过程中需要临时存储的值。
• 因此，空间复杂度是 O(1)，表示算法使用的空间量不随输入数据的大小而变化。

五、总结知识点

1. 二维数组（矩阵）操作：代码处理的是一个二维数组（矩阵），这是算法设计中常见的数据结构。在 Java 中，二维数组可以看作是数组的数组。

2. 循环结构：代码使用了嵌套的 for 循环来遍历矩阵的元素。外层循环用于控制旋转的层次，内层循环用于在每一层中进行元素的交换。

3. 原地算法（In-place Algorithm）：这个算法在不使用额外空间的情况下，直接在输入的矩阵上进行操作，即原地旋转。这是优化算法空间复杂度的一种常用方法。

4. 边界处理：在旋转矩阵时，只有最外层的元素需要交换。因此，代码通过计算层数 layers 来确定需要处理的边界。

5. 临时变量：在交换元素时，使用临时变量 top 来保存被覆盖的值，这是在进行元素交换时常见的技巧，以避免信息丢失。

6. 数学计算：代码中的 offset 变量用于计算当前元素在旋转后的新位置。这涉及到对矩阵索引的数学计算。

7. 条件判断：在内层循环中，i 和 first 的差值 offset 被用来确定元素在旋转后的新位置，这是基于矩阵的对称性质。

8. 旋转操作：顺时针旋转 90 度的操作，实际上是对矩阵的四个边界进行元素交换，这是一种典型的矩阵旋转操作。

以上就是解决这个问题的详细步骤，希望能够为各位提供启发和帮助。