网站建设时设置语言选项免费生成短链接

原题链接

难度：$easy$

---

题目描述

统计一个数字在排序数组中出现的次数。

示例 1:

输入: nums = [5,7,7,8,8,10], target = 8
输出: 2

示例 2:

输入: nums = [5,7,7,8,8,10], target = 6
输出: 0

提示：

• $0<=nums.length<=10^5$
• $-10^9<=nums[i]<=10^9$
• $nums$ 是一个非递减数组
• $-10^9<=target<=10^9$

注意：

• 本题与主站 34 题相同（仅返回值不同）：https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/

• 面试官出这题的话肯定是想让你写二分的啦 其他没用。

• 给面试官说有两种类型的解法，一种是暴力，一种是二分法求边界，体现递进的思考过程，别上来一言不发写个二分，失去一个表现机会。

• 对于二分法，我们可以分别求左边界和右边界，也可以二分求左边界之后接着遍历计数，两种情况对应在真实场景下连续相等的数据一般有多长。如果经常出现很长一串连续相等的数据，就用二分法求右边界，否则容易使算法退化到
  O(n)。

• 分析完了之后，给一个规范的解法，注意函数驼峰式命名这些能体现你专业性的小细节

---

算法1

(模拟)

创建一个变量 ans，扫描整个数组，如果数组中的值等于 target，那么 ans 就加一，最后输出答案。

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是数组的长度。需要遍历数组一次。

• 空间复杂度 : $O(1)$，只需要常数空间存放若干变量。

C++ 代码

class Solution {
public:int search(vector<int>& nums, int target) {int ans = 0;for (int i = 0; i < nums.size(); i ++) {if (nums[i] == target)ans ++;}return ans;}
};

---

---

算法2

(二分)

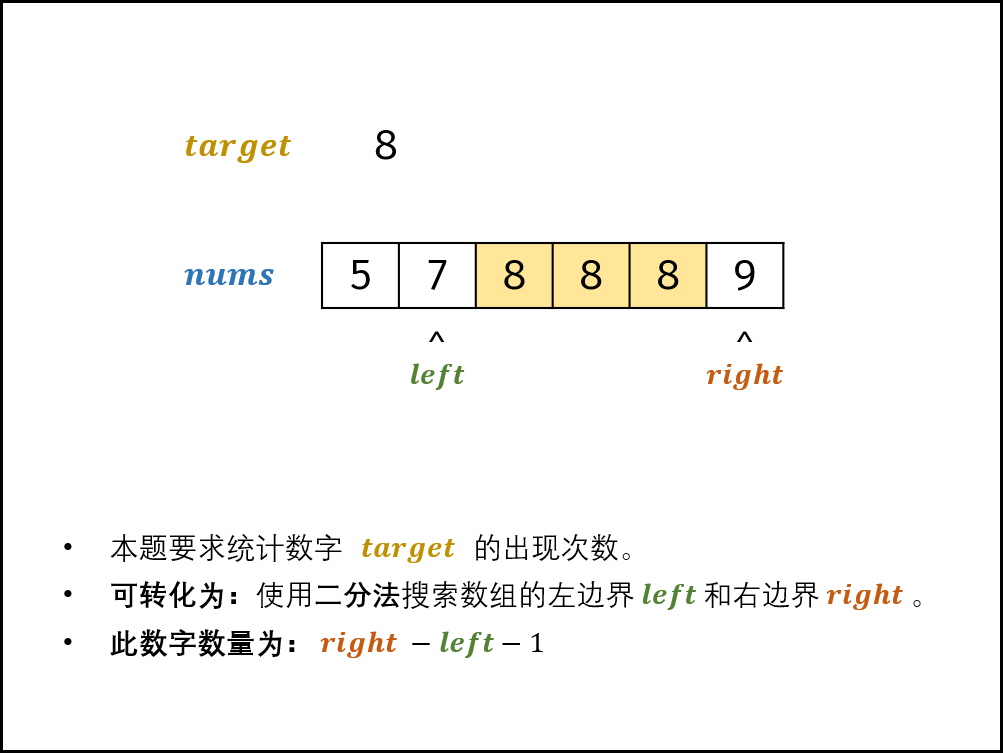
• 排序数组 nums 中的所有数字 target 形成一个窗口，记窗口的 左 / 右边界 索引分别为 left 和 right ，分别对应窗口左边 / 右边的首个元素。

• 本题要求统计数字 target 的出现次数，可转化为：使用二分法分别找到 左边界 left 和 右边界 right ，易得数字 target 的数量为 right−left−1 。

复杂度分析

• 时间复杂度：$O(logn)$，二分法为对数级别复杂度。

• 空间复杂度 : $O(1)$，几个变量使用常数大小的额外空间。

C++ 代码

class Solution {
public:int search(vector<int>& nums, int target) {if (nums.size() == 0) return 0;int l = 0, r = nums.size() - 1;int ans = 0;//寻找最左边的下标while (l < r) {int mid = (l + r) / 2;if (nums[mid] >= target)r = mid;else l = mid + 1;}if (nums[l] != target) return ans;int left = l;l = 0, r = nums.size() - 1;//寻找右边的下标while (l < r) {int mid = (l + r + 1) / 2;if (nums[mid] <= target)l = mid;else r = mid - 1;}int right = l;ans = right - left + 1;return ans;}
};

---