舌尖上的西安 网站怎么做seo费用
一、树
非线性数据结构,在实际场景中,存在一对多,多对多的情况。

树( tree)是n (n>=0)个节点的有限集。当n=0时,称为空树。
在任意一个非空树中,有如下特点。
1.有且仅有一个特定的称为根的节点。
2.当n>1时,其余节点可分为m (m>0)个互不相交的有限集,每一个集合本身又是一个树,并称为根的子树。
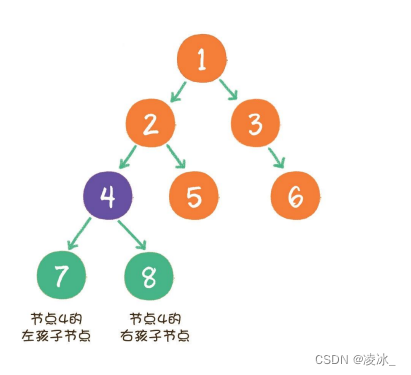
如图所示:节点1:根节点(root),节点5,6,7,8:叶子节点(leaf);分为不同的层级,节点4是父节点(parent),节点4的孩子节点(child)节点4的兄弟节点(sibling);

树的最大的层级树,称为数的高度或深度,上图的数的高度为4。
二、 二叉树
二叉树(binary tree)是树的一种特殊形式。二叉顾名思义,这种树的每个节点最多有2个孩子节点。
注意:这里是最多有2个,也可能只有1个,或者没有孩子节点。
二叉树节点的两个孩子节点,一个被称为左孩子(leftchild) ,一个被称为右孩子(right child)。
此外,二叉树还有两种特殊形式,一个叫作满二叉树,另一个叫作完全二叉树。
2.1、二叉树的五种基本形式:
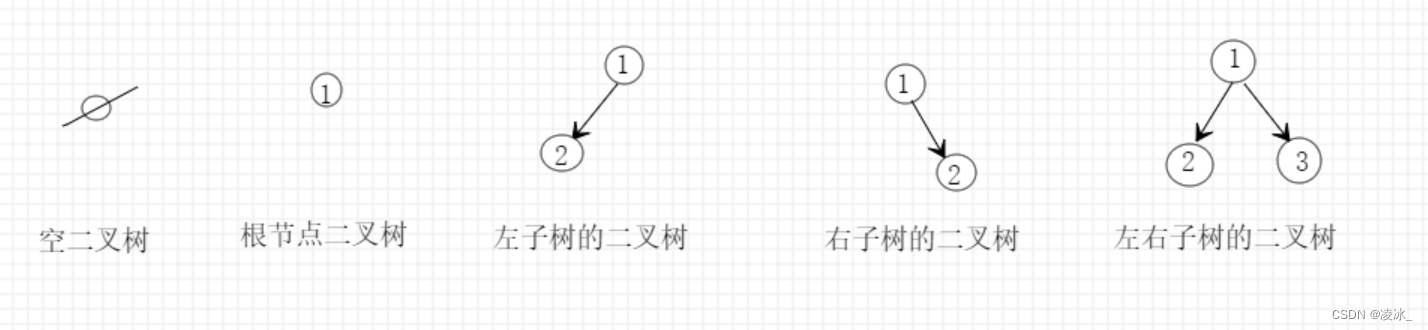
2.2、二叉树与树的区别 :
- 树中结点的最大度数没有限制,而二叉树结点的最大度数为2
- 树的结点无左、右之分,而二叉树的结点有左、右之分
2.3、满二叉树与完全二叉树:
(1)满二叉树
一个二叉树的所有非叶子节点都存在左孩子和右孩子,并且所有叶子节点都在同一层级上,那么这个树就是满二叉树。
简单点说,满二叉树的每一个分支都是满的。

(2)完全二叉树
对一个有n个节点的二叉树,按层级顺序编号,则所有节点的编号为从1到n。如果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同,则这个二叉树为完全二叉树。

在上图中,二叉树编号从1到12的12个节点,和前面满二叉树编号从1到12的节点位置完全对应。因此这个树是完全二叉树。
完全二叉树的条件没有满二叉树那么苛刻:满二叉树要求所有分支都是满的;而完全二叉树只需保证最后一个节点之前的节点都齐全即可。
三、二叉树的性质
1、在二叉树的第 i 层上最多有 2^n-1个结点(i>=1)
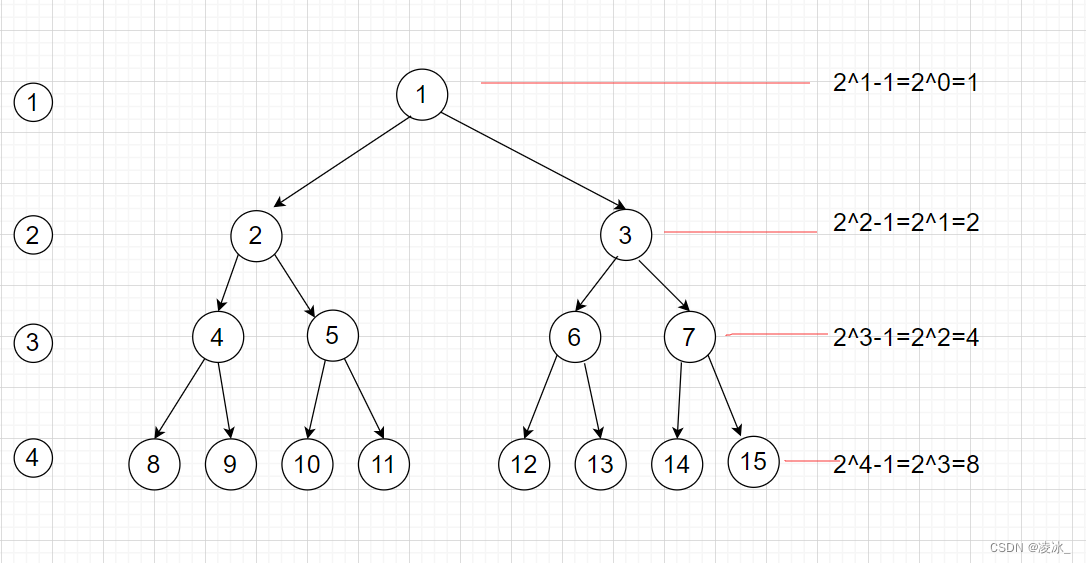
2、深度(高度)为 k 的二叉树最多有 2^k - 1个结点(k>=1)

3、对任意一颗二叉树,如果其叶子节点数为 N0,度为2的结点数为N2,则 N0 = N2 + 1
设 : 结点之间的总连线数是B ,总结点数是n,
度为0的结点是n0,
度为1的结点是n1,
度为2的结点是n2,
从上往下看 二叉树最大的度就是2所以的节点要么度是2,要么度是1,要么度是0,度是2的会发出两条线, 度是1的发出1条线所以得到图片里的公式 B = n2 * 2 + n1;
二叉树的总结点数 n = n1 +n2+n0;
总连续数 B=n-1

由此得出:度是0的结点个数=度是2的结点个数+1
四、二叉树的存储
1.链式存储结构
2.数组
(1)链式存储结构

- 存储数据的data变量
- 指向左孩子的left指针
- 指向右孩子的right指针
(2)数组
使用数组存储时,会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺,则数组的相应位置也空出来。

如何方便地在数组中定位二叉树的孩子节点和父节点?
假设一个父节点的下标是parent,
左孩子节点的下标=2xparent +1;
右孩子节点的下标=2xparent+2。
由此:
如果一个左孩子节点的下标是leftChild,那么它的父节点下标=(leftChild-1)/2。
如果一个右孩子节点的下标是rightChild,那么它的父节点下标=(rightChild-2)/2。
图上所示, 节点5的索引是4,那么节点5的父节点=(4-2)/2=1,由此可得索引1对应的是节点2
五、二叉树的遍历
- 深度优先遍历
- 广度优先遍历
1. 深度优先遍历
深度优先( depth first search,DFS ) ,顾名思义就是偏向于纵深,“一头扎到底”的访问方式。深度优先遍历又根据遍历顺序的不同分为三种:前序遍历、中序遍历、后序遍历。
1.1 前序遍历
所谓前序遍历,是指二叉树遍历每个子树的时候,都是按照根结点、左子树、右子树的顺序来遍历,因为根结点在前,所以叫做前序遍历。前序遍历中根结点的优先级别最高。如下图所示:

1.2 中序遍历
如果二叉树遍历每个子树的时候,都是按照左子树、根结点、右子树的顺序来遍历,因为根结点在中间,所以叫做中序遍历。如下图所示:

1.3 后序遍历
二叉树遍历每个子树的时候,都是按照左子树、右子树、根结点的顺序来遍历,因为根结点在最后,所以叫做后序遍历。如下图所示:

使用递归的方式来操作,如图所示

''''树节点'''
class TreeNode:'''初始化'''def __init__(self,data):self.data=data #数据self.left=None #左节点self.right=None #右节点'''二叉树'''
class MyTree:def create_tree(self,input_list=[]):#判断数列是否为空if input_list is None or len(input_list)==0:return None#第一个出队data=input_list.pop(0)#判断数据为空if data is None:return None#树节点node=TreeNode(data)#创建左节点node.left=self.create_tree(input_list)#创建右节点node.right =self.create_tree(input_list)return nodedef before_foreach(self,node):'''前序遍历 (根左右):param node: 二叉树节点:return:'''# 判断节点为空if node is None:return None#显示节点数据print(node.data,end=',')#再次遍历左节点,右节点self.before_foreach(node.left)self.before_foreach(node.right)return nodedef middle_foreach(self,node):'''中年序遍历 (左根右):param node: 二叉树节点:return:'''# 判断节点为空if node is None:return None#再次遍历左节点self.middle_foreach(node.left)# 显示节点数据print(node.data, end=',')# 再次遍历右节点self.middle_foreach(node.right)return nodedef after_foreach(self,node):'''后序遍历 (左右根):param node: 二叉树节点:return:'''# 判断节点为空if node is None:return None#再次遍历左节点,右节点self.after_foreach(node.left)self.after_foreach(node.right)# 显示节点数据print(node.data, end=',')return nodeif __name__ == '__main__':#二叉树对象my=MyTree()#列表ll=list([5,6,8,None,None,10,None,None,9,None,7])#调用方法node=my.create_tree(input_list=ll)print('前序遍历')my.before_foreach(node)print('\n中序遍历')my.middle_foreach(node)print('\n后序遍历')my.after_foreach(node)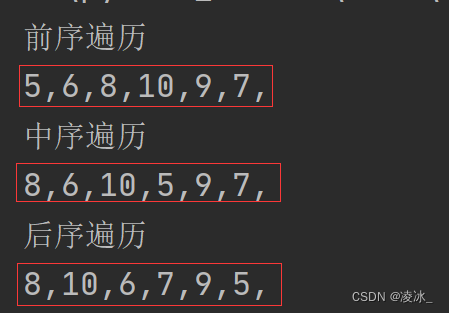
2. 广度优先遍历
广度优先遍历( Breadth First Search,BFS )也叫层序遍历,就是按照二叉树中的层次从左到右依次遍历每层中的结点。层序遍历的实现思路是利用队列来实现。
先将树的根结点入队,然后再让队列中的结点出队。队列中每一个结点出队的时候,都要将该结点的左子结点和右子结点入队。当队列中的所有结点都出队,树中的所有结点也就遍历完成。此时队列中结点的出队顺序就是层次遍历的最终结果。如下图所示:

(1) 根节点1入队列

(2) 节点1出队,输出节点1,并得到节点1的左孩子节点2、右孩子节点3。让节点2和节点3入队。
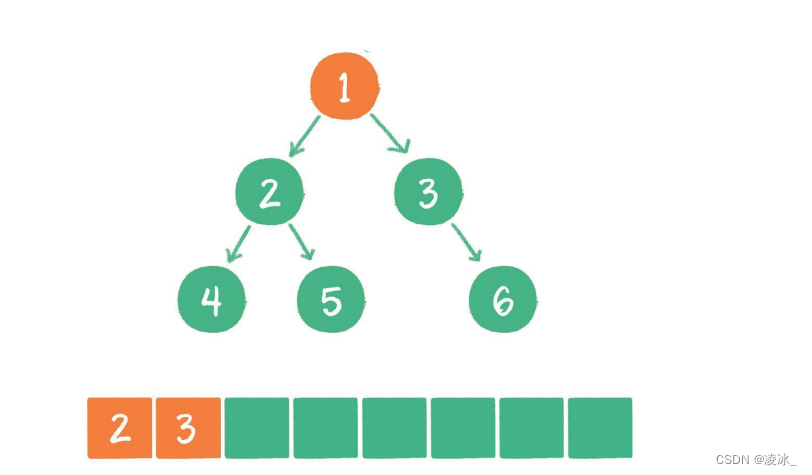
(3) 节点2出队,输出节点2,并得到节点2的左孩子节点4、右孩子节点5。让节点4和节点5入队。

(4) 节点3出队,输出节点3,并得到节点3的右孩子节点6。让节点6入队。

(5)节点4出队,输出节点4,由于节点4没有孩子节点,所以没有新节点入队。
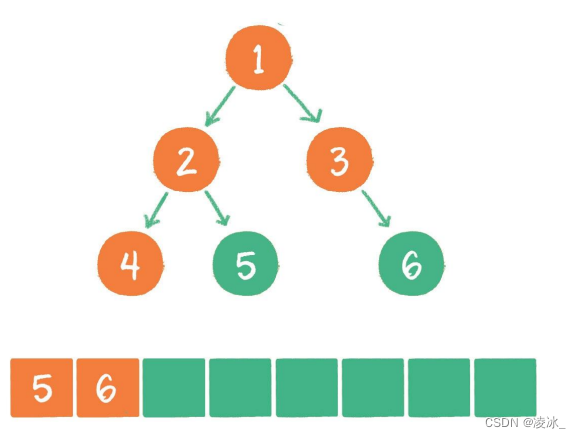
(6)节点5出队,输出节点5,由于节点5同样没有孩子节点,所以没有新节点入队。
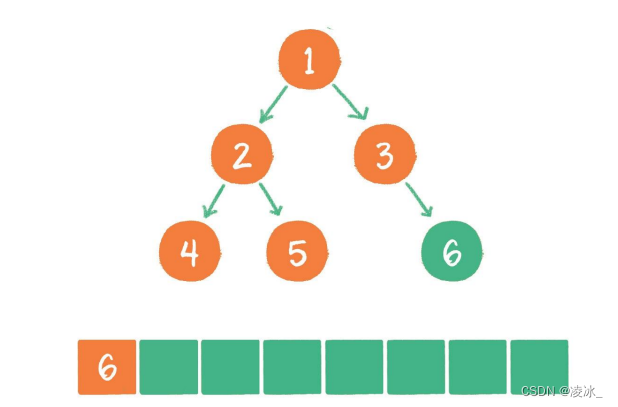
(7) 节点6出队,输出节点6,节点6没有孩子节点,没有新节点入队。
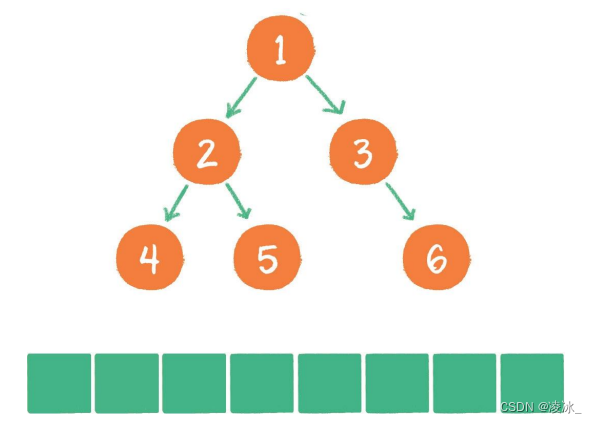
使用递归的方式来操作,如上图所示
'''节点'''
class TreeNode:'''初始化数据'''def __init__(self, data):self.data = dataself.left = Noneself.right = None'''层序遍历'''
def level_order_traversal(root):# 判断节点为空if root is None:return []#数列result = []#队列queue = [root]#循环while queue:level = [] #层列#循环for _ in range(len(queue)):#第一个数据出队列node = queue.pop(0)#添加数据level.append(node.data)#判断左节点是否不为空if node.left is not None:queue.append(node.left)# 判断左节点是否不为空if node.right is not None:queue.append(node.right)#添加到列表中result.append(level)return resultif __name__ == '__main__':#二叉树对象root = TreeNode(1)root.left = TreeNode(2)root.right = TreeNode(3)root.left.left = TreeNode(4)root.left.right = TreeNode(5)root.right.right = TreeNode(6)print(level_order_traversal(root)) 
在实际应用中,二叉树又是使用最广泛的,特别是二叉树的几种遍历操作的规则,需要重点掌握。在面试或应试中,通常会根据前序、中序、后序中的两种序列,询问另外一种树的遍历结果。
