当前位置： 首页 > news >正文

百度网盘怎么做网站黑五类广告推广

news 2025/7/6 1:43:54
百度网盘怎么做网站,黑五类广告推广,教育投资网站建设方案,新网站多久被收录补题链接： Week 3 DAY 1-CSDN博客 河南萌新联赛2024第（二）场：南阳理工学院-CSDN博客 Week 3 DAY 5:-CSDN博客 Week 3 DAY 6-CSDN博客 这周题单是动态规划——（背包问题，线性dp）&#xff1a…

补题链接：

Week 3 DAY 1-CSDN博客

河南萌新联赛2024第（二）场：南阳理工学院-CSDN博客

Week 3 DAY 5:-CSDN博客

Week 3 DAY 6-CSDN博客

这周题单是动态规划——（背包问题，线性dp）：

这周对背包问题有了百分之三十的理解 ^-^,区间dp听的牛客的，没听懂，将就写着了，后面还会出一个与区间dp相关的周报，这里有点乱七八糟的。。。.不过下面的背包问题和线性dp的知识点我觉得我记录的还可以，嘻嘻╮(. ❛ ᴗ ❛.)╭，了解到一些知识点的名称——SG函数，最小生成树，KMP,KMP学了，掌握进度百分之20吧。晕晕的 o(￣ヘ￣o#)
 

注意：

1009-「木」迷雾森林_动态规划专题：线性dp、背包问题，区间 (nowcoder.com)

注意：这代替开long long 会爆空间；因为内存空间是还得乘上字节数；

区间dp:

2955 -- Brackets (poj.org)

括号匹配：

f[i][j]表示ai....aj的串中，有多少个已经匹配的括号

如果ai与ak是匹配的

f[i][j]=max(f[i][j],f[i+1][k-1]+f[k+1][j]+2)——>2是自己匹配的括号

相当于是将 i 到 j 分成  [xxxxx]  xxxxxx两部分

否则，f[i][j]=f[i+1][j];

(将第一个元素去掉---因为它肯定不能算)

边界f[i][j]=0;

记忆化搜索：

如果用递推的话，应该是区间大小由小到大递增作为最外层循环

for(int l=2;l<=n;l++)//枚举区间长度

{

for(int i=0;i+l-1<n;i++)//枚举区间起点

{

int j=i+l-1;//枚举区间终点

}

}

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<string>
using namespace std;
char a[105];
int dp[105][105];
int main()
{while(scanf("%s",a)!=EOF){       if(a[0]=='e'){return 0;}int n = strlen(a);memset(dp,0,sizeof(dp));for(int len = 2;len<=n;len++){for(int i = 0;i+len-1<=n-1;i++){int j = i+len-1;if((a[i]=='('&&a[j]==')')||(a[i]=='['&&a[j]==']')){dp[i][j] = max(dp[i][j],dp[i+1][j-1]+2);}for(int k = i;k<=j;k++){dp[i][j] = max(dp[i][j],dp[i][k]+dp[k+1][j]);}    }   }printf("%d\n",dp[0][n-1]);}return 0;
}

 最长回文子序列

516. 最长回文子序列 - 力扣（LeetCode）

1.马拉车方法

2.动态规划：f[i][j]表示ai.....aj的串中，最长回文子序列长度

如果ai与 aj是一样的

f[i][j]=f[i+1][j-1]+2；

如果不一样，就要删掉其中一个

石子合并

石子合并 (nowcoder.com)

拓展：石子合并问题（动态规划）_石子合并问题动态规划-CSDN博客

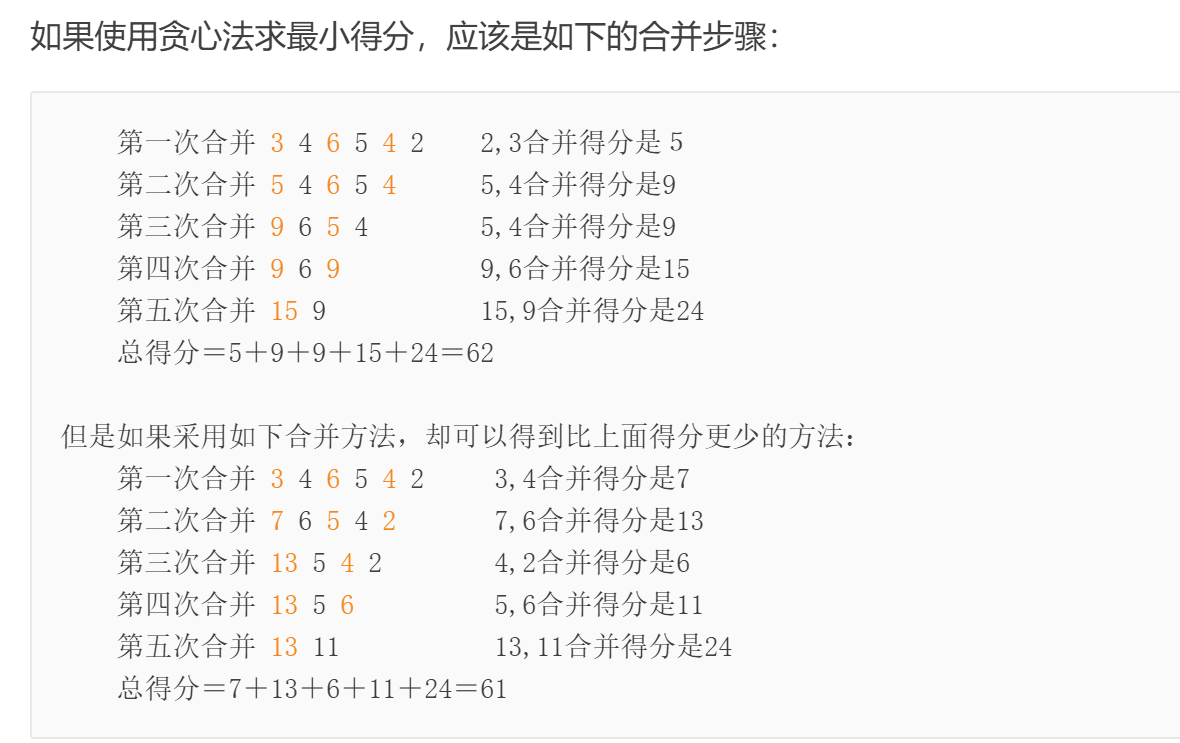
  1. 先考虑没有环的
  2. f[i,j]表示合并 i 到 j 的所有石子的得分·；
  3. f[i,j]=max(f[i][j],f[i+k]+f[k+1][j]+sum[i][j]->(sum[j]-sum[i-1]);
  4. sum[i][j]表示i到j的石子的价值和！（也可以前缀和实现sum【i】表示前i个石头的价值，那么我们需要的就是sum[j]-sum[i-1]）
  5. 但是现在有环！——可以通过取模的方法把他变成循环的！
  6. 也可以将序列加倍：变成：“1234 1234”，就可以完全用链的方法解决了！
  7. 边界：f[i][j]=0;                                                                                                                                                                        

凸多边形的三角形拆分

凸多边形的划分 (nowcoder.com)

 不会

田忌赛马

田忌赛马 (nowcoder.com)

田忌只有两种选择；1.田忌用最强的马打，2.田忌用最弱的马打

所以可以定义为区间，

f[k][i][j];后k轮比赛中，田忌使用了第i到第j匹马能够获得的最多的钱

k=1;i=1;j=n;

k=2;i=2 ;j=n/  i=1;j=n-1;

n-j+i=k;

(用过的马)j-i+1=n-k+1；

max:

  • 齐王 第k匹马 和田忌 第i匹马 结果+f[k+1][i+1][j];
  • 齐王 第k匹马 和田忌 第i匹马 结果+f[k+1][i][j-1];

只带i，j 可以省掉k。

#include <bits/stdc++.h>using namespace std;
#define int long long
const int maxn = 10001;
int n;
int dp[maxn][maxn];
int tian[maxn];
int qi[maxn];int cost(int tian_pos, int qi_pos) {if (tian[tian_pos]>qi[qi_pos]) return 200;if (tian[tian_pos]<qi[qi_pos]) return -200;if (tian[tian_pos]==qi[qi_pos]) return 0;return 0;
}signed main() {cin>>n;for (int i=1;i<=n;i++) {cin>>tian[i];}for (int i=1;i<=n;i++) {cin>>qi[i];}sort(qi+1, qi+1+n);sort(tian+1, tian+1+n);for (int len = 1;len<=n;len++) {for (int l=1;l+len-1<=n;l++) {int r = l+len-1;int k = len-1+1;dp[l][r] = max(dp[l+1][r]+cost(l, k), dp[l][r-1]+cost(r,k));}}cout<<dp[1][n];return 0;
}作者：在刷题的单身狗很开心
链接：https://www.nowcoder.com/discuss/542652396985442304
来源：牛客网

背包DP

N个物品，容量为V,每个物品有他的价值vi和权重wi（每个物品只能用一次或0次）；

01背包问题（每件物品只能最多用一次）:

2. 01背包问题 - AcWing题库

dp：

右边那一块不一定有，可能会出现空集，比如;

当列举的 j 此时小于某件物品的 v 时,就装不下，此时右边的结果就没有

 二维：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int v[1005],w[1005];
int dp[1005][1005];
signed main(){int N,V;cin>>N>>V;for(int i=1;i<=N;i++){cin>>v[i]>>w[i];}for(int i=1;i<=N;i++){for(int j=0;j<=V;j++){dp[i][j]=dp[i-1][j];if(j>=v[i]){dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);}}}cout<<dp[N][V];return 0;
}

一维：

二维时的更新方式是：

	dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);

 为何能转化为1维？

我们发现对于每次循环的下一组i,只会用到 i-1来更新当前的值，不会用到 i-2及其之后的值。于是可以在这次更新的时候，将原来的更新掉，反正以后也用不到。所以对于 i 的更新，只需要一个数组直接覆盖就行。

2.我们发现，对于每次 j 的更新，只需用到之前 i-1时的 j 或者j-v[i],不会用到之前后面的值，所以为了防止串着改，我们采取从后往前更新的方式，用原来 i-1的数组更新 i ;(如果从前往后更新的话，前面的更新过之后，会接着更新后面的值，这样就不能保证是原来的 i-1的数组来更新 i 的了

#include<bits/stdc++.h>
using namespace std;
#define int long long
int v[1005],w[1005];
int dp[1005];
signed main(){int N,V;cin>>N>>V;for(int i=1;i<=N;i++){cin>>v[i]>>w[i];}for(int i=1;i<=N;i++){for(int j=V;j>=v[i];j--){dp[j]=max(dp[j],dp[j-v[i]]+w[i]);}}cout<<dp[V];return 0;
}

完全背包（每件物品有无数个）；

3. 完全背包问题 - AcWing题库

类似01背包问题，

 朴素做法会超时：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int v[1005],w[1005];
int f[1005][1005];
signed main(){int N,V;cin>>N>>V;for(int i=1;i<=N;i++){cin>>v[i]>>w[i];}for(int i=1;i<=N;i++){for(int j=1;j<=V;j++){for(int k=0;k*v[i]<=j;k++){f[i][j]=max(f[i-1][j],f[i-1][j-k*v[i]]+k*w[i]);}}}cout<<f[N][V]<<endl;return 0;
}

 优化：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int v[1005],w[1005];
int f[1005][1005];
signed main(){int N,V;cin>>N>>V;for(int i=1;i<=N;i++){cin>>v[i]>>w[i];}for(int i=1;i<=N;i++){for(int j=0;j<=V;j++){f[i][j]=f[i-1][j];if(j-v[i]>=0)f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);}}cout<<f[N][V]<<endl;return 0;
}

 一维

这里的 j 不去要从大到小枚举，因为它要的不是i-1的状态，它要的是当前 i 的状态

#include<bits/stdc++.h>
using namespace std;
#define int long long
int v[1005],w[1005];
int f[1005][1005];
signed main(){int N,V;cin>>N>>V;for(int i=1;i<=N;i++){cin>>v[i]>>w[i];}for(int i=1;i<=N;i++){for(int j=0;j<=V;j++){//if(j-v[i]>=0)f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i]);else f[i][j]=f[i-1][j];}}cout<<f[N][V]<<endl;return 0;
}

 整理一下：

01背包和完全背包的不同之处

01背包：

 完全背包：

多重背包（每个物品数量不一样）；

朴素暴力解法

4. 多重背包问题 I - AcWing题库

#include<bits/stdc++.h>
using namespace std;
const int N=220;
int n,m;
int v[N],w[N],s[N];
int f[N][N];
int main(){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;k<=s[i]&&k*v[i]<=j;k++){f[i][j]=max(f[i-1][j],f[i-1][j-v[i]*k]+w[i]*k);}}}cout<<f[n][m];
}

 多重背包不能用完全背包的优化方式，因为完全背包个数是无数个，多重背包个数是有限个没所以写式子的时候就是

已知第二段式子的最大值，并不能求出第二段除红色框以外的最大值，所以这种方法不可取

比如  知道两个绿色的最大值并不能知道粉色线的最大值。所以就不能直接用完全背包的方式优化

 用二进制方式优化：

用10个新的物品表示原来的i个物品

这10个物品就是

2 4 8 16 32 64 128 256 512 1024

可以拼凑第i个物品所有的方案数了

log（n）;

具体的就是：

s=200;

1，2，4，8，16，32，64,    73

 可以凑出的数;

1，3，7，15, 31 , 63,   127   200  

s:n

1 2 4 8..... 2^k , C  (C<2^(k+1));

时间复杂度是N*V*logS;

做一遍01背包：

让他自己组数字，找出最大价值；

如果仍然不是很能理解的话，取这样一个例子:要求在一堆苹果选出n个苹果。我们传统的思维是一个一个地去选，选够n个苹果就停止。这样选择的次数就是n次

二进制优化思维就是：现在给出一堆苹果和10个箱子，选出n个苹果。将这一堆苹果分别按照1,2,4,8,16,.....512
1，2，4，8，16，512
分到10个箱子里，那么由于任何一个数字x∈[0,1023]
𝑥∈[0,1023] (第11个箱子才能取到1024)都可以从这10个箱子里的苹果数量表示出来，但是这样选择的次数就是 ≤10次。

#include<bits/stdc++.h>
using namespace std;
const int N=25000;
int n,m;
int v[N],w[N];
int f[N];
int main(){cin>>n>>m;int cnt=0;for(int i=1;i<=n;i++){int a,b,s;cin>>a>>b>>s;//a是第i种物品的体积，b是第i种物品的价值，//s是第i种物品的数量int k=1;while(k<=s){//进行二进制分组cnt++;v[cnt]=a*k;//第cnt组的体积就是一个物品的体积乘以cnt组的数量w[cnt]=b*k;//价值同理s-=k;//将s拆分k*=2;}if(s>0){//算C;cnt++;v[cnt]=a*s;w[cnt]=b*s;}}n=cnt;for(int i=1;i<=n;i++){//01背包问题：怎么从这n种中选择最大的价值；//这n种可以组成0-s的数字其中一个；for(int j=m;j>=v[i];j--){f[j]=max(f[j],f[j-v[i]]+w[i]);}	}cout<<f[m]<<endl;return 0;}

分组背包问题（物品有n种，每种物品有若干个，只能选一组物品）；

  和多重背包的思考方式是一样的；

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n,m;
int v[N][N],w[N][N],s[N];
int f[N];
int main(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>s[i];for(int j=0;j<s[i];j++){cin>>v[i][j]>>w[i][j];}}for(int i=1;i<=n;i++){for(int j=m;j>=0;j--){for(int k=0;k<s[i];k++){if(v[i][k]<=j){f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);}	}}}cout<<f[m]<<endl;return 0;}

 线性DP:

一行一行的求,难在分类

数字三角形：

898. 数字三角形 - AcWing题库

初始化的时候列要多初始化一格

#include<bits/stdc++.h>
using namespace std;
const int N=505;
int n,m;
int a[N][N],w[N][N],s[N];
int f[N];
int main(){int n;cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cin>>a[i][j];}}for(int i=0;i<=n;i++){for(int j=0;j<=i+1;j++){//这里要多初始化一点w[i][j]=-1e9;}}w[1][1]=a[1][1];for(int i=2;i<=n;i++){for(int j=1;j<=i;j++){w[i][j]=max(w[i-1][j-1]+a[i][j],w[i-1][j]+a[i][j]);}}int res=-1e9;for(int i=1;i<=n;i++){res=max(res,w[n][i]);}cout<<res<<endl;return 0;}

 895. 最长上升子序列 - AcWing题库

最长上升子序列

这里分类的是以第i个数结尾；

什么是子序列？

可以隔着挑，但是得从前往后挑；

 最长上升子序列的长度等于f[j]+1(1是后面以i结尾的那个数);

a[i]=max(a[j]+1);aj<ai (j=0,1,.....i-1);

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int n,m;
int a[N],w[N][N],s[N];
int f[N];
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){f[i]=1;//只有a[i]一个数的情况for(int j=1;j<i;j++){if(a[i]>a[j]){f[i]=max(f[i],f[j]+1);}}}int res=0;for(int i=1;i<=n;i++){res=max(res,f[i]);}cout<<res<<endl;return 0;
}

怎么记录最长子序列有那些数？

 用一个数组g[i]去记录每一个长度转移的状态。

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int n,m;
int a[N],w[N][N],g[N];
int f[N];
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){f[i]=1;//只有a[i]一个数的情况g[i]=0;for(int j=1;j<i;j++){if(a[i]>a[j]){if(f[i]<f[j]+1){f[i]=f[j]+1;g[i]=j;//记录转移}}}}int k=1;for(int i=1;i<=n;i++){if(f[k]<f[i]){k=i;}}cout<<f[k]<<endl;for(int i=0,len=f[k];i<len;i++){cout<<a[k];k=g[k];//这里是倒着输出的}return 0;
}

最长公共子序列

897. 最长公共子序列 - AcWing题库

 

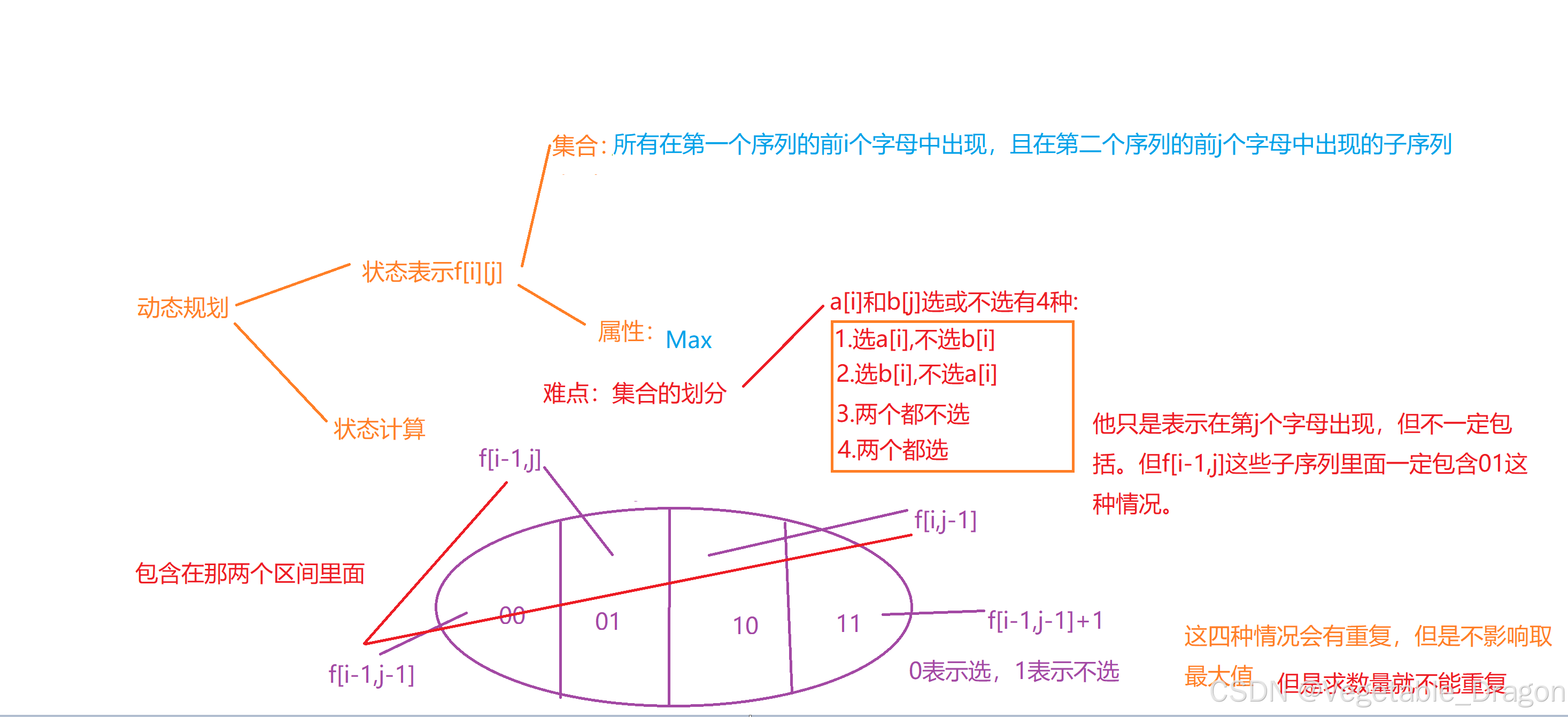
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int n,m;
char a[N],w[N][N],b[N];
int f[N][N];
int main(){cin>>n>>m;scanf("%s%s",a+1,b+1);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){f[i][j]=max(f[i-1][j],f[i][j-1]);if(a[i]==b[j]){f[i][j]=max(f[i][j],f[i-1][j-1]+1);}}}cout<<f[n][m]<<endl;return 0;
}

 ;

这周增添的讲题环节，虽然说能多多少少听懂一些学姐学长的思路，但是毕竟知识点跨度较大，我觉地，emmmm......可能对我帮助没有那么大，再者就是讲题的时候，有些同学更注重讲解如何去做题，其实，题意讲述明白也是很重要的哇T-T。有些东西光听是记不住的，过几天也就忘了，但是星期五晚上的牛客讲题是好的，毕竟题目都看过了也有所思考，以我们目前的水平补充点知识是能做的，就是看不懂题解，学长讲了题目的算法有哪些，可以私下再去填充，然后上手补题，我觉地这是很好的，至于星期六晚上的那堂课，呜呜呜，算法小白有种高一生听高考题的感觉，其实我就觉的我们目前还是得把基础打牢一点吧，先不要去试图建立高楼，有些东西听了也就只是听过，要实实在在的得到东西还是得通过练习，听后有练习才是听课的价值所在。T-T

over:

先到这吧，bye~

http://www.hengruixuexiao.com/news/22452.html

相关文章：

  • 石排镇网站建设公司搜索引擎入口大全
  • 福建漳州东山规划建设局网站如何做网站设计
  • wordpress 本机安装windows优化大师下载安装
  • 外汇局网站怎么做延期收款报告惠州短视频seo
  • 做网站实例torrentkitty磁力天堂
  • 做海外市场什么网站推广24小时最新国际新闻
  • 那些网站做推广bt磁力在线种子搜索神器
  • 自己怎样做免费网站百度快照在哪里
  • 做网站pyton怎么建个网站
  • 广东英德网站建设全网优化哪家好
  • 公司网站封面怎么做防恶意点击软件
  • 网站制作哪些公司好创建一个网站
  • 建设网站的步骤知乎郑州seo顾问热狗
  • 网站后台管理员做链接上海搜索seo
  • 金融网站源码 asp线下推广渠道和方式
  • 海口网站建设兼职sem是什么?
  • 网络广告管理办法西安搜索引擎优化
  • 昆明网站建设.com网络seo啥意思
  • 在乐文网站做翻译靠谱吗网站推广方法有哪些
  • 国外做的好看的网站设计专业的郑州网站推广
  • 响应式模板苏州网站优化公司
  • 跑腿个人网站怎么做广州网站设计制作
  • 商城网站做推广方案怎么做自己的网站
  • 网站建设销售提成建设一个网站的具体步骤
  • 东莞网站制作网站线上营销平台有哪些
  • 先做网站还是先做appapp推广注册接单平台
  • 中国建设银行官网站e路护航快速排名程序
  • 手机就可以直接做设计的网站百度seo排名优化教程
  • 有没有做语文题的网站百度关键词搜索广告的优缺点
  • 知名购物网站有哪些百度seo排名优化公司哪家强