前言：前面学习了顺序表，队列，栈，链表，我们知道他们都是一种线性表，是一种线性结构，而除此之外，仍有许多我们还没认识的结构，比如树形结构，不同于线性结构，树形结构就如同他的名字，结构相对更加复杂，是一种倒着的树的数据结构。

目录

1，什么是树？

2.树的相关概念 

3.树的定义

4.二叉树

 特殊的二叉树：

2.二叉树的存储方式

5.堆

结构体定义与函数接口

堆的初始化

堆的销毁

入堆

向上调整算法

向下调整算法

出堆

---

1，什么是树？

树是一种非线性的数据结构，它是由n(n>0)个有限节点组成一个具有层次关系的集合，把它叫做书是因为它看起来像一颗倒挂着的树（个人感觉也像树根部的形状），也就是他是根朝上，叶子朝下。

树结构拥有自己的一些独特性质：

.有一个特殊的节点，称为根节点，根节点没有前驱节点

.除根结点外，其余节点被分为M（M>0）个互不相交的集合T1,T2,......Tm，其中每个集合我们可以认为也是一个类似主树的子树，每个子树的节点有且只有一个前驱，可以有0或多个后继节点。

.树是递归定义的，因为它的套娃结构，大树里住着小树。

如下图一根秃了的倒着的树与树结构的对比

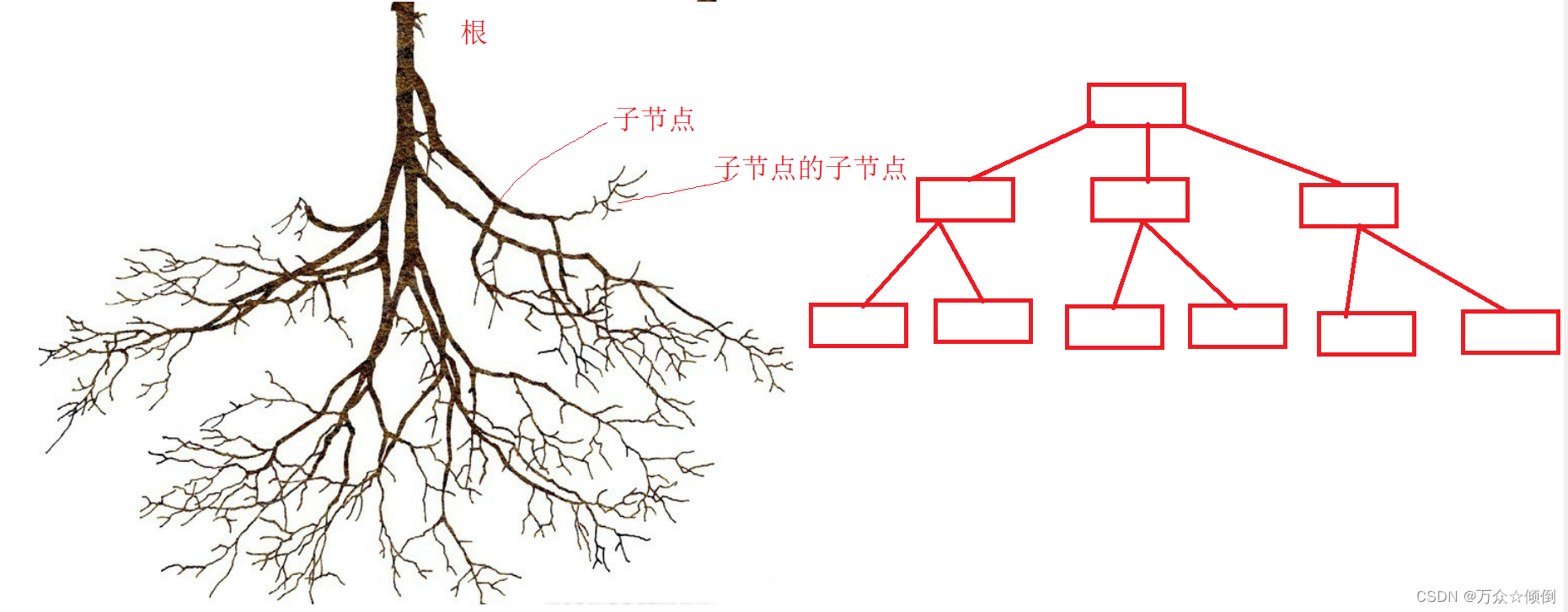
 注意：树型结构里面是不能出现子树相交的

不仅仅对于树形结构是这样，树也不能出现一个枝干长到另一个枝干上（可能存在变异）。

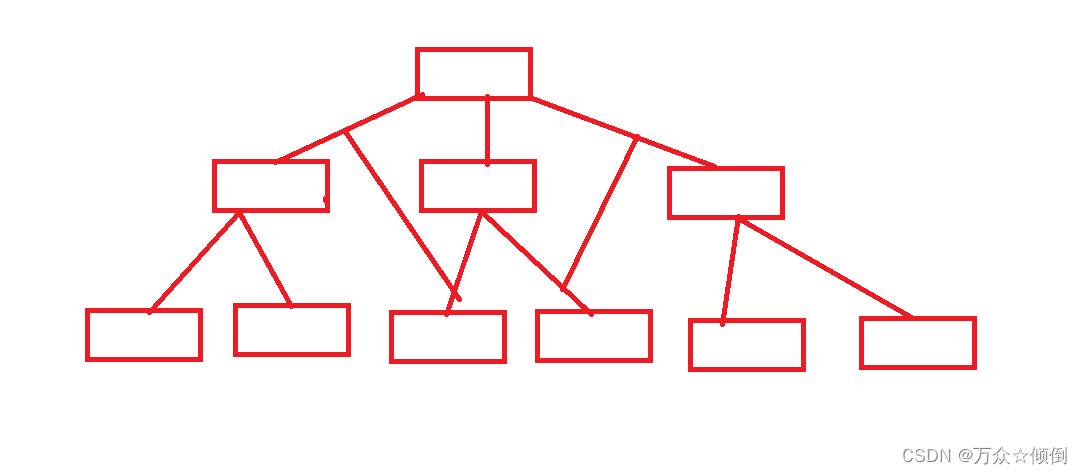
2.树的相关概念 

树的某些相关概念是以人类的血缘关系为样例所命名：

我们知道树是一种非线性的数据结构，它是由n（n>=0）个结点的有限集合。

当n=0时称为空树。在任何一棵非空树中：1. 有且只有一个特定的称为 根（root） 的结点；2. 当n>1时，其余结点可分为m（m>0）个 互不相交 的有限集，其中每一个集合又是一棵树，并且成为 根的子树（subtree） 。

结点的度：结点拥有的子树数称为结点的 度（Degree）如上图D的度为3，A度为2.

树的度： 是树内各结点的度的最大值。如D为3

度为0的结点成为 叶节点（Leaf） 或者 终端结点 ，除根结点外，分支结点也称为 内部结点 。如上图的G H I。

结点子树的根称为该结点的 孩子（Child）。如A的孩子B,C

相应的该结点称为孩子的 双亲（Parent） 。如D的双亲为B

同一个双亲之间的孩子之间互称为 兄弟（Sibling）。B与C互为兄弟

结点的 祖先 是指从根到该结点所经历的所有结点.

反之，以该结点为根的子树中的任意一结点称为该节点的 子孙 。

树的层次：从根开始，根为第一层，根的节点为第二层，以此类推。

树的深度：树中结点的最大层次称为树的 深度（Depth） 或者高度，根据树中结点是否可以交换分为有序树和无序树。

堂兄弟节点：双亲在同一层的节点互为堂兄弟。如D,E。

森林 ：是指的多棵互不相交的树。

路径和路径长度： 树中两个结点之间的 路径 是由这两个结点之间所经过的结点序列构成的，而 路径长度 是路径上所经过的 边的个数 。

3.树的定义

因为树有很多节点，按照之前的链表他们定义结点的方法，没接触前树我们可能这样定义：

struct TreeNode
{int data;struct  TreeNode*child1;struct  TreeNode*child2;
//......
}

但其实不太可能。人们总结了许多定义树的结构的方法：

1.如果明确了树的度，那么可以定义。（根据树的度来定义节点个数，但是不太能表现树）

2.用顺序表来存放孩子。

struct TreeNode
{int data;Seqlist   childArr;
}

3.双亲表示法。（每个位置只存储该节点的父节点）：用数组存放双亲的下标。

并查集这里就是只存储父亲的下标。

4.左孩子右兄弟方法：比较牛的一种方法，也是一种较优的方法：每一个节点只存放他的第一个孩子节点和下一个兄弟节点。

struct TreeNode{struct TreeNode*firstchid;//第一个孩子节点struct TreeNode*nextbrother;//指向下一个兄弟节点int data;//节点的数据域}

 对于森林，一般是文件系统结构。

4.二叉树

概念：一种特殊的树的结构，一个二叉树是节点的一个有限集合：

1.要么为空

2.有一个根节点加上两个子树（左右子树）组成。如图：

 我们可以看到：

1.二叉树不存在度大于2的节点

2.二叉树有左右之分，左边的节点叫左孩子，右边的节点叫右孩子，次序不能颠倒，因此是一个有序树。

 特殊的二叉树：

1.满二叉树

概念：一个二叉树，如果每层结点数都达到最大值，那么这个树就是满二叉树。也就是说，如果一个二叉树的层数为K，那么总结点数为，（2^k）-1),等比求和公式可推导出，第N层的节点数为2^(n-1).

2.完全二叉树

概念：相对于满二叉树的最后一行，最后一行不全满，且结点依次从左到右，就是一个完全二叉树。

若一个完全二叉树的层数为k，那么他的k-1层以上的每一层都是满的。

满二叉树是一种特殊的完全二叉树。

若深度为h,节点范围【2^(h-1),2^h-1】.

2.二叉树的存储方式

1.可用二叉链表来表示（有的地方是三叉链表，多了一个结点指向前面的双亲）。

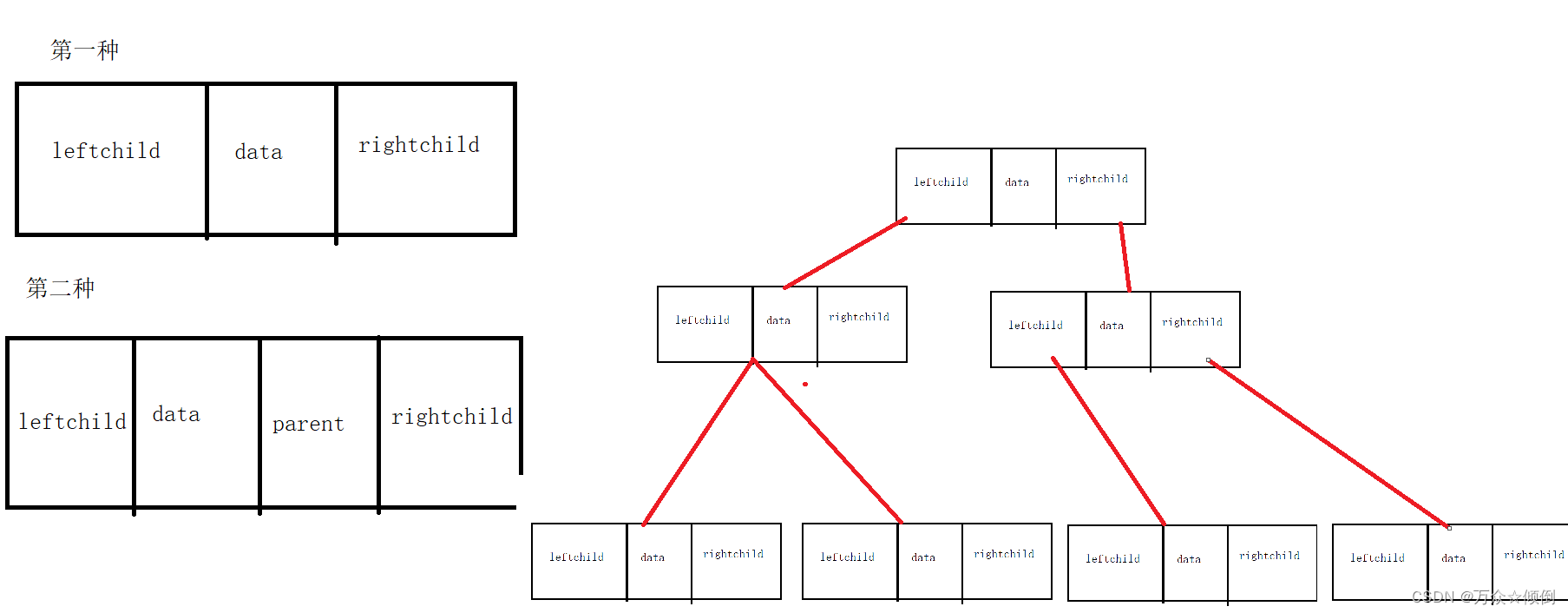
2.可用数组来表示。

 用数组存放右几个优点：

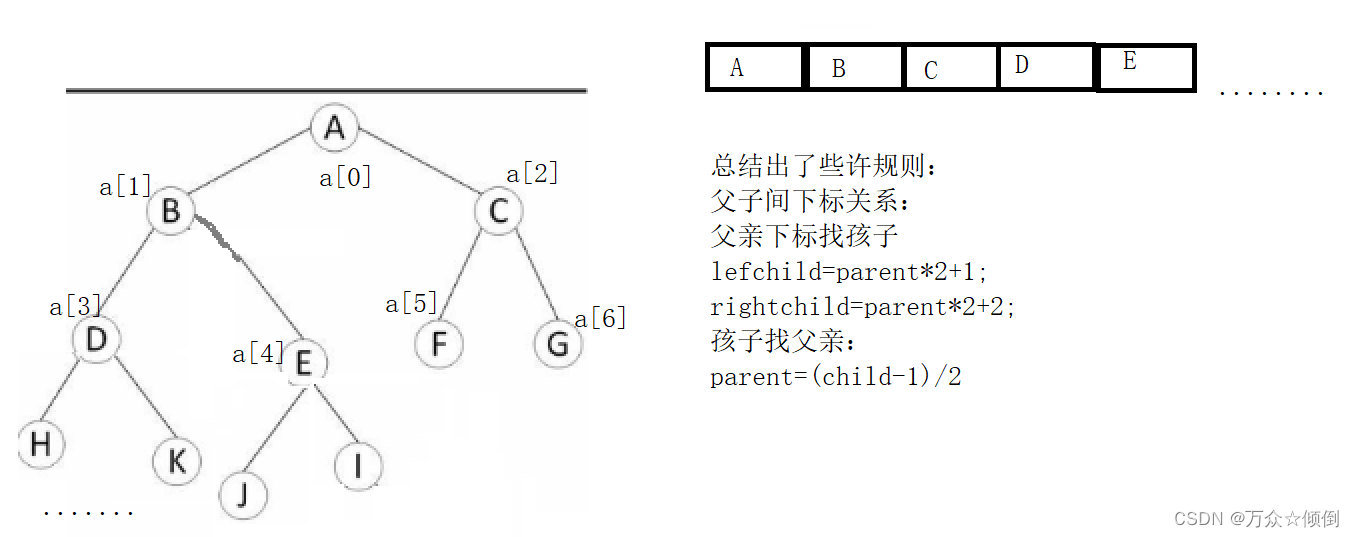
 对于这种存储，比较适合完全二叉树来存储。，因为若有一个双亲没有孩子节点，对于数组这种下表表示双亲存在问题。

5.堆

知道以上的存储方法，对于完全二叉树，有一个叫做堆的结构，堆本质就是一个完全二叉树，

堆分两种：1.大堆    2.小堆

除了是完全二叉树，大堆需满足任何一个双亲都大于等于孩子，对于小堆，任何一个双亲都小于等于孩子。

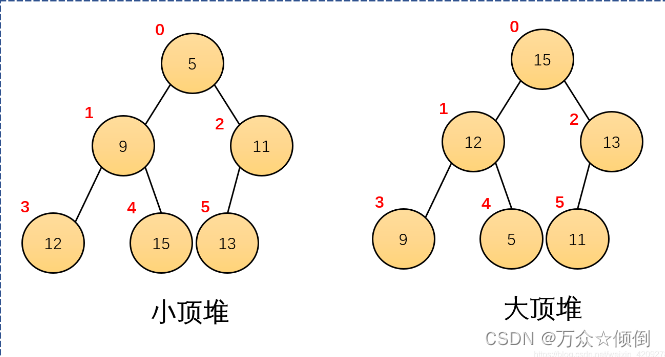
我们实现堆就用数组来实现的：这里以实现小堆为例

结构体定义与函数接口

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int HPDATAtype;
typedef struct Heap
{HPDATAtype *a;int size;int capacity;
}HP;void Heapinit(HP* f);
void Heapdestroy(HP* f);
void Heappop(HP* f);
void Heappush(HP* f , HPDATAtype x);

堆的初始化

void Heapinit(HP* f)
{//初始有4个空间assert(f);f->a = NULL;f->size = 0;f->capacity = 0;
}

堆的销毁

void Heapdestroy(HP* f)
{assert(f->a);free(f->a);f->a = NULL;
}

入堆

void Heappush(HP* f, HPDATAtype x)
{assert(f);if (f->capacity == f->size){int  newcapacity = f->capacity = 0 ? 4 : f->capacity*2;HPDATAtype* newnode = (HPDATAtype*)malloc(newcapacity);if (newnode == NULL){perror("扩容失败\n");return;}f->a = newnode;f->capacity = f->capacity*2;}f->a[f->size] = x;f->size++;//向上调整算法Adjustup(f->a, f->size - 1);//向下调整算法//Adjustdown(f->a, f->size - 1);
}

在这里在入堆之后，也就是元素赋值到数组之后，根据你对数组的调整，也就是所说的向上调整算法，和向下调整算法，决定是小堆，还是大堆。

向上调整算法

我们这里通过对树所对应的数组元素的关系寻找父亲。

void Adjustup(HPDATAtype*a, int child)
{//根据孩子zhaofuqinint parent = (child - 1) / 2;while (child>0){if ( a[child]<a[parent]){HPDATAtype p = a[child];a [child] = a[parent];a[parent]=p;child = parent;parent = (child - 1) / 2;}else {break;}}
}

向下调整算法

void Adjustdown(HPDATAtype* a, int child)
{//根据孩子找父亲int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){int tmp = a[child];a[child] = a[parent];a[parent] = tmp; child = parent;parent = (child - 1) / 2;}else{break;}}}

出堆

出堆就是最后一个元素换到第一个元素，在size--，之后在进行调整。

void Heappop(HP* f){assert(f);//堆顶元素出堆,最小元素出堆assert(f->size);int tmp = f->a[0];f->a[0] = f->a[f->size - 1];f->a[f->size - 1] = tmp;f->size--;//向上调整for (int i = 0; i < f->size; i++){Adjustup(f->a, i);}
};

堆的应用：

优先级队列的实现     堆排序算法    获取特定范围的值